Integrales definidas por sustitución – Cambio de los límites de integración
Krystian Karczyński
Fundador y jefe del servicio eTrapez.
Maestro en Matemáticas por la Universidad Tecnológica de Poznań (Polonia). Tutor de matemáticas con muchos años de experiencia. Creador de los primeros Cursos eTrapez, que se han vuelto enormemente populares entre estudiantes de toda Polonia.
Vive en Szczecin (Polonia). Le gusta caminar por el bosque, ir a la playa y hacer kayak.
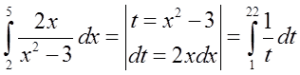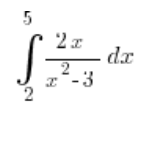
Para abordar el problema mostrado arriba sobre la integración definida, necesitamos usar la sustitución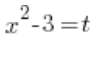 
, y todos estamos de acuerdo aquí. Pero, ¿qué pasa con los límites de integración?
Límites de integración en tareas de sustitución para integrales definidas
¿Podemos escribir:
?
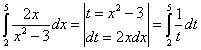Por supuesto que no. El problema con los límites de integración. En la integral definida a la izquierda, se relacionan con la variable 
, y a la derecha con la variable 
, por lo tanto, también deben cambiar con la variable.
Una solución (que recomiendo en mi curso) es evitar completamente el problema, resolviendo la integral indefinida (sin límites de integración) por separado y luego insertando los límites de integración 5 y 2 en el resultado (con la variable x).
La segunda solución es enfrentar el problema directamente y cambiar los límites de integración de acuerdo con la sustitución. Dado que los límites en la variable x son 2 y 5, después de la sustitución: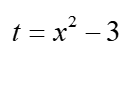 
serán en la variable t respectivamente 1 y 22, y obtuve estos resultados sustituyendo 2 y 5 por x en la sustitución 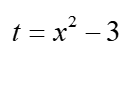. Por lo tanto, el paso correcto sería:
¿Buscas clases particulares de matemáticas para nivel universitario o de secundaria? ¿O quizás necesitas un curso que te prepare para el examen de selectividad?
Somos el equipo de eTrapez. Enseñamos matemáticas de manera clara, sencilla y muy detallada - llegamos incluso al más resistente al aprendizaje.
Hemos creado cursos en video explicados en un lenguaje comprensible para descargar en tu computadora, tableta o teléfono. Enciendes la grabación, miras y escuchas, como en las clases particulares. A cualquier hora del día o de la noche.
