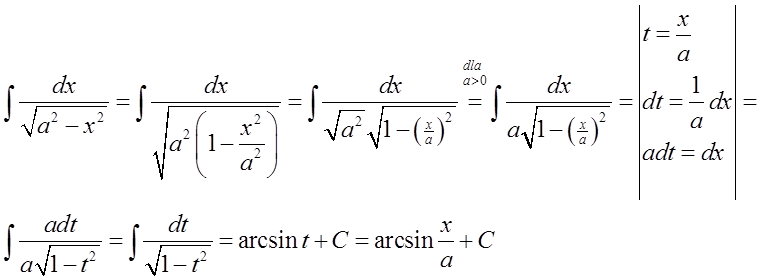Fórmulas Prohibidas para Integrales Indefinidas – Derivación de las Fórmulas

---

Los profesores en las universidades tienen sus propias exigencias. Muchos de ellos, por el bien de sus estudiantes, por supuesto, no dudan en especificar con mucho detalle las reglas sobre cómo deben resolverse los problemas.

Un usuario de mi Curso de Integrales Indefinidas me escribió en GG así:

Tengo una petición, ¿podría usted en su FB o blog mostrar cómo se derivan las integrales en sus fórmulas a la forma del papel? Me refiero a las fórmulas No.: 5, 9, 10, 13, 14, 15, 16. Desafortunadamente, nuestra profesora nos dijo que solo se pueden utilizar las más simples, las más complejas que mencioné hay que descomponerlas uno mismo a la forma dada. Creo que mucha gente se lo agradecería 🙂

Se refiere a la hoja con las fórmulas adjunta al Curso:

Fórmulas para Integrales Indefinidas

Y concretamente a las siguientes fórmulas:

5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}

 

9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}

 

10.\quad \int{ctgxdx=\ln \left| \sin x \right|}+C

 

13.\quad \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}

 

14.\quad \int{\frac{dx}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{2a}\ln \left| \frac{x-a}{x+a} \right|+C}

 

15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}

 

16.\quad \int{\frac{dx}{\sqrt{{{x}^{2}}+q}}=\ln \left| x+\sqrt{{{x}^{2}}+q} \right|+C}

 

Si no son estos, son otros

Sí, es verdad, los profesores a menudo exigen usar estas fórmulas específicas y no otras. O no usar algunas fórmulas en absoluto. O usar las que no nos gusta usar.

La única salida razonable en tales situaciones, por supuesto, es la completa sumisión. En la sala de examen, el profesor es la ley y no tiene sentido quejarse más tarde a los amigos de que el profesor no aprobó el coloquio, aunque “debería haberlo hecho”.

En lugar de eso, revisaré las fórmulas mencionadas punto por punto y mostraré cómo manejar cada caso individualmente (desafortunadamente, no se pueden “abarcar” con alguna regla común). “Manejar”, significa resolver integrales que requieren usar esa fórmula sin usar esa fórmula, sino usando una fórmula menos general, o derivando la integral por sustitución o de manera racional.

Entonces, una por una:

5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}

Con esta fórmula, en realidad no sé cuál es el problema, se deriva directamente de invertir la fórmula de la derivada:

{{\left( {{a}^{x}} \right)}^{\prime }}={{a}^{x}}\ln a

Así que aquí no muestro completa sumisión al profesor, sino que pido una explicación de cómo demonios calcular \int{{{3}^{x}}dx} sin usar la fórmula \int{{{a}^{x}}dx}.

Si alguien tiene una idea interesante, por favor compártala con la humanidad en los comentarios debajo de la publicación.

9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}

De acuerdo, volvemos al juego.

Esta fórmula no se deriva directamente de invertir ninguna fórmula de la derivada.

Si acordamos que no la conocemos, podemos calcular la integral \int{tgxdx} por sustitución:

10.\quad \int{ctgxdx=\ln \left| \sin x \right|}+C

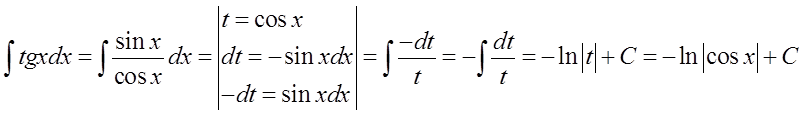
Aquí, de manera análoga a la anterior:

13.\quad \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}

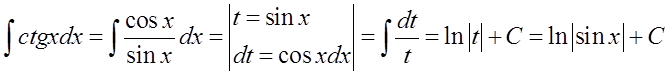
Esta fórmula es una forma general de la fórmula:

\int{\frac{dx}{{{x}^{2}}+1}=arctgx+C} o: \int{\frac{dx}{1+{{x}^{2}}}=arctgx+C}

Al profesor le interesa que usemos la fórmula: \int{\frac{dx}{{{x}^{2}}+1}=arctgx+C} (que resulta de invertir una fórmula de la derivada), y no usar la fórmula: \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C} (que ya es una fórmula “procesada”).

Lo hacemos de la siguiente manera (por transformación y sustitución):

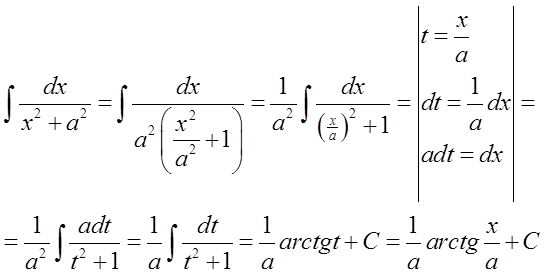
En un ejemplo específico, podría verse así:

14.\quad \int{\frac{dx}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{2a}\ln \left| \frac{x-a}{x+a} \right|+C}

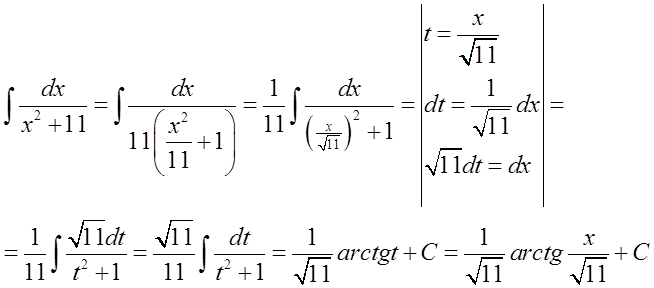
Esta fórmula es diferente a la anterior, no se trata de usar una fórmula en la que en lugar de ‘a’ hay ‘1’ (tal fórmula no existe). La alternativa a usar esta fórmula aquí es hacer una descomposición en fracciones parciales como en los integrales racionales (mostré cómo se hace en la Lección 5 del Curso de Integrales Indefinidas).

De hecho, \frac{1}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{\left( x-a \right)\left( x+a \right)} y puede descomponerse aún más en fracciones parciales. Por ejemplo:

\frac{1}{{{x}^{2}}-9}=\frac{1}{\left( x-3 \right)\left( x+3 \right)} \frac{1}{\left( x-3 \right)\left( x+3 \right)}=\frac{A}{x-3}+\frac{B}{x+3}

Luego multiplicamos por \left( x-3 \right)\left( x+3 \right), calculamos las constantes A, B comparando polinomios y todo como se muestra en la Lección 5 del Curso.

15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}

Aquí nuevamente, la fórmula general: \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C} debe transformarse en la fórmula específica: \int{\frac{dx}{\sqrt{1-{{x}^{2}}}}=\arcsin x+C}.

Lo hacemos de manera similar a la fórmula 13):

En un ejemplo específico, podría verse así:

16.\quad \int{\frac{dx}{\sqrt{{{x}^{2}}+q}}=\ln \left| x+\sqrt{{{x}^{2}}+q} \right|+C}

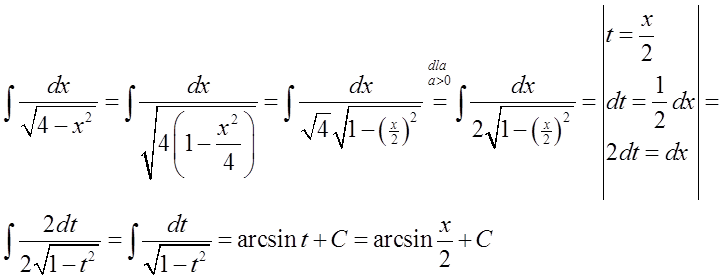
El asunto es más complicado, requiere el uso de las llamadas “sustituciones hiperbólicas” (seno y coseno hiperbólicos). Dejo este tema en esta publicación, pero seguramente escribiré sobre estas sustituciones pronto.

Estas son las fórmulas que preguntó el usuario, y añadiré que los añadidos a la lista de fórmulas básicas por mí:

\int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C \int{\sin axdx}=-\frac{1}{a}\cos ax+C \int{\cos axdx}=\frac{1}{a}\sin ax+C

Se derivan por simple sustitución: t=ax

Así que, por ejemplo, teniendo la integral: \int{{{e}^{-x}}dx} y NO pudiendo usar (debido a las preferencias del profesor) la fórmula \int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C, usamos la sustitución t=-x y continuamos tranquilamente el cálculo.