El Rango de una Matriz con un Parámetro
Krystian Karczyński
Fundador y jefe del servicio eTrapez.
Maestro en Matemáticas por la Universidad Tecnológica de Poznań (Polonia). Tutor de matemáticas con muchos años de experiencia. Creador de los primeros Cursos eTrapez, que se han vuelto enormemente populares entre estudiantes de toda Polonia.
Vive en Szczecin (Polonia). Le gusta caminar por el bosque, ir a la playa y hacer kayak.
Vamos a calcular el rango de la matriz:
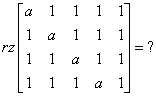
Solución
Puedes abordar esto de varias maneras, y probablemente la forma más rápida es multiplicar la quinta columna por -1 y sumarla a la primera, segunda, tercera y cuarta columna, obteniendo así:
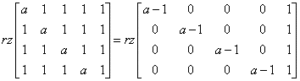Ahora, tomemos el determinante de la matriz de cuarto grado:
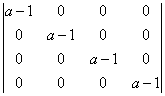Un determinante donde todos los elementos excepto la diagonal principal son cero es igual al producto de los elementos en la diagonal principal (algún día lo demostraré 🙂 ), por lo tanto:
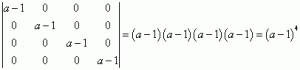Este determinante es diferente de cero para todos los a distintos de 1. Por lo tanto, para esos a, el rango de nuestra matriz, que necesitamos calcular, es 4 (porque se puede extraer un menor no nulo de cuarto grado, y no se puede obtener uno mayor).
¿Qué pasa con el caso en el que 
. Entonces obtenemos el rango de la matriz (sustituyendo a por 1):
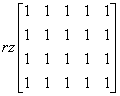Y este rango es 1 (puedes, por ejemplo, nuevamente usar la quinta columna sobre las demás y eliminar las columnas cero).
Por lo tanto, para a distinto de 1, el rango de la matriz es 4, y para a igual a 1, el rango de la matriz es 1.
¿Buscas clases particulares de matemáticas para nivel universitario o de secundaria? ¿O quizás necesitas un curso que te prepare para el examen de selectividad?
Somos el equipo de eTrapez. Enseñamos matemáticas de manera clara, sencilla y muy detallada - llegamos incluso al más resistente al aprendizaje.
Hemos creado cursos en video explicados en un lenguaje comprensible para descargar en tu computadora, tableta o teléfono. Enciendes la grabación, miras y escuchas, como en las clases particulares. A cualquier hora del día o de la noche.
