Esta publicación está dedicada a un fragmento de una pregunta de examen de bachillerato que me envió un estudiante por correo electrónico. Sin embargo, vale la pena echar un vistazo por curiosidad y no repetir nunca más que las matemáticas en la universidad son más difíciles que las matemáticas avanzadas en la escuela secundaria.
🙂
Parte del Problema
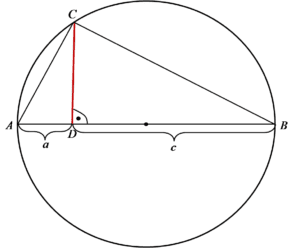
Tenemos la siguiente situación:
Es necesario mostrar que el segmento marcado en rojo tiene una longitud de 
. Por supuesto, esto es solo una pequeña parte de todo el problema. ¿Adivinen de qué se trata? De sucesiones por supuesto 🙂
Entonces, aquí podemos usar un truco muy común en problemas con la altura del triángulo rectángulo, usando los triángulos similares que son los «favoritos» de todos los estudiantes de bachillerato.
1. Los triángulos 
(el más pequeño) y 
(el más grande, inscrito en el círculo) son similares (tienen 2 ángulos iguales: recto y <DAC, por lo que el tercer ángulo también es igual, lo que significa que tenemos semejanza AA). Los triángulos 
(el mediano) y (el más grande de nuevo) también son similares (tienen 2 ángulos iguales: recto y <CBD, por lo que el tercer ángulo también es igual, lo que significa que tenemos semejanza AA de nuevo). Si los triángulos y son similares a , entonces también son similares entre sí y eso es lo que notamos:
es similar a
2. Si estos triángulos son similares, entonces las proporciones de los lados CORRESPONDIENTES serán iguales. Por supuesto, elegimos las proporciones que contienen el segmento rojo, cuya longitud denotamos como 
.
En el triángulo la proporción del lado MÁS CORTO por el lado MEDIO será igual a:
En el triángulo la proporción del lado MÁS CORTO por el lado MEDIO será igual a:
Dado que los triángulos son similares, hay una igualdad:
3. De esta igualdad, resolvemos h, la longitud del segmento rojo. Multiplicamos cruzado como en proporciones y obtenemos:
Lo que significa:
Que es exactamente lo que necesitábamos mostrar al principio. BINGO.
La moraleja es: al determinar la altura en un triángulo rectángulo (la que cae sobre la hipotenusa por supuesto), a menudo necesitamos usar la semejanza de triángulos, como arriba.
Y otra es que las matemáticas avanzadas en la escuela secundaria realmente podían ser difíciles. Solo en la universidad podemos respirar fácilmente 🙂
