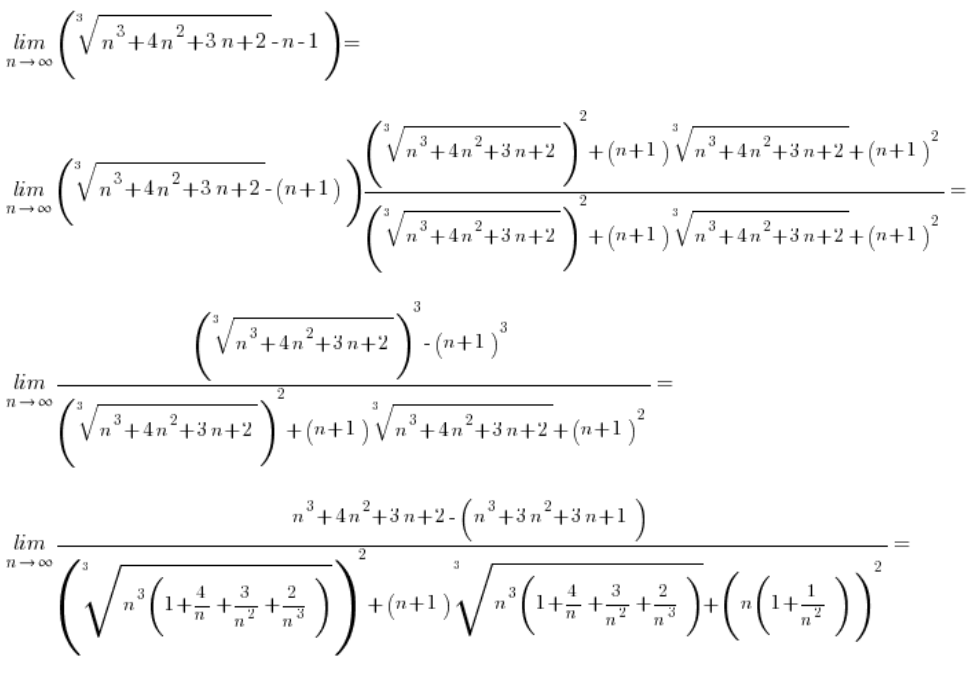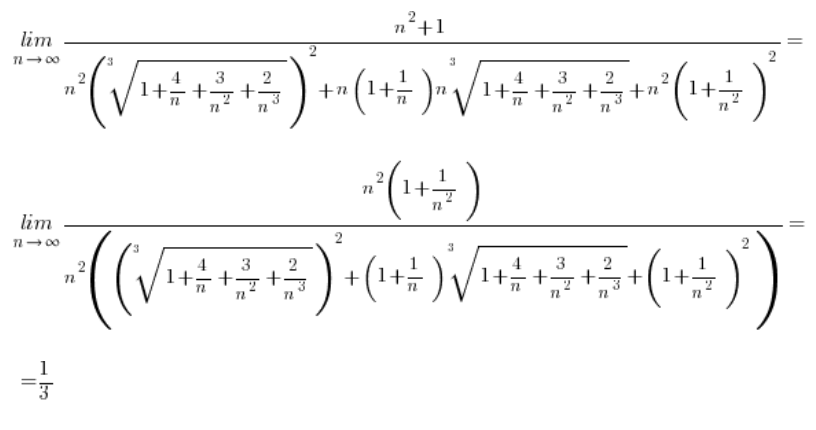Límites con raíces cúbicas (¿Es multiplicación por el conjugado?)

---

¿Cómo se veía con raíces “normales”?

Cuando teníamos un límite para calcular, que involucraba alguna resta con una raíz (y que obviamente no se podía calcular de manera más simple), es decir:

“ALGO – raíz de algo”

“raíz de algo – ALGO”

“raíz de algo – raíz de algo”

usábamos un truco que yo llamo – “multiplicación por el conjugado”.

Simplemente multiplicábamos esta expresión por su contraparte con un signo más, o más bien por una fracción donde esta contraparte estaba en el numerador y el denominador.

Por ejemplo:

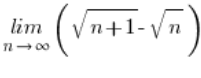 lo multiplicábamos así: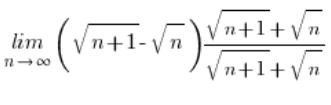

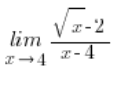lo multiplicábamos así: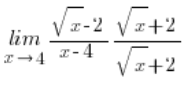

Este truco inteligente nos permitía llegar al patrón de la fórmula de multiplicación abreviada:

Una vez que alcanzamos este patrón, los cuadrados “eliminaban” las raíces y llegábamos a la solución simple (bueno, a veces una solución simple un poco más larga).

Pero, ¿qué pasa cuando las raíces involucradas en la resta son raíces cúbicas? Como aquí, por ejemplo:

\underset{x\to 8}{\mathop{\lim }}\,\frac{\sqrt[3]{x}-2}{x-8}

El método estándar de proceder, es decir, multiplicar de la siguiente manera:

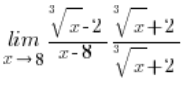
No nos servirá de nada, porque esta vez en el numerador, después de llegar al patrón:

Los cuadrados no “eliminarán” las raíces cúbicas de ninguna manera. Así que seguiremos atascados.

¿Cómo será con las raíces cúbicas?

En el caso de la resta con raíces cúbicas, simplemente tenemos que “apuntar” a un patrón completamente diferente (pero también de la escuela secundaria), es decir:

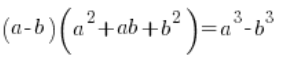
Entonces, nuestro dado (donde a o b o ambos son raíces cúbicas) en lugar de multiplicar por multiplicaremos por y después de aplicar el patrón, los cubos harán su trabajo, “eliminando” las raíces.

Ejemplo 1

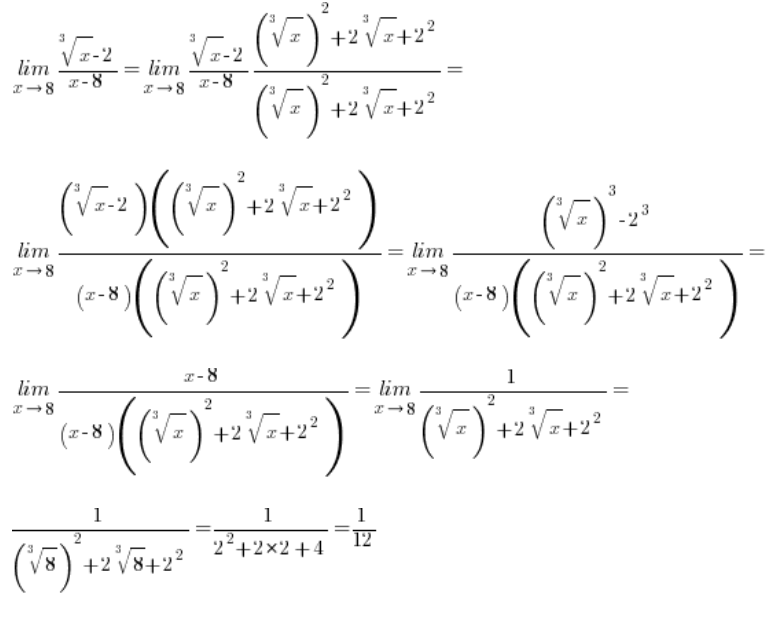
Ejemplo 2