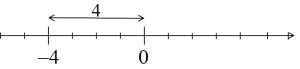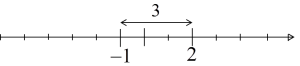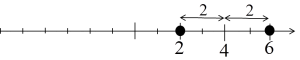Si has estado estudiando matemáticas en la universidad por un tiempo, seguramente habrás notado que la mayoría del material cubierto en la escuela secundaria no te es directamente útil en la universidad. Si apenas estás comenzando a estudiar, presta atención a esto.
¿Qué significa «directamente»?
Digo «directamente» porque, obviamente, cada gota de tu sudor matemático en la secundaria no se desperdiciará y se contará para ti. Estoy hablando de ejercitar el pensamiento abstracto, la capacidad de concentrarse en un problema y cosas así.
Sin embargo, sinceramente, no necesitarás volver a muchos de los temas de matemáticas que se cubrieron en la escuela secundaria, ni siquiera para echarles un vistazo y repasar.
Pero hay excepciones.
Hay cosas que se cubren en la escuela secundaria, sin cuyo conocimiento no llegarás muy lejos en la universidad.
Al comienzo del año académico, vale la pena repasarlas o simplemente aprenderlas. De esta manera, abrirás el camino para nuevos temas. Si no las repasas, te molestarán constantemente, como una espina en el zapato, dificultando (o incluso imposibilitando) tu progreso.
No serán grandes áreas de matemáticas, sino más bien pequeños detalles, pequeños ladrillos, sin los cuales toda la estructura podría colapsar.
Definición de límite
Tomemos por ejemplo la definición de límite de una sucesión, con la que te encontrarás muy pronto:
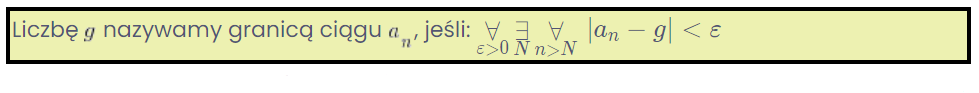
¿Entiendes esos extraños símbolos a la izquierda? ¿Y ese valor absoluto a la derecha? ¿No mucho?
Y sin embargo, para entender o al menos leer correctamente esta definición, debería ser suficiente conocer los cuantificadores (esas criaturas a la izquierda: ![]() ) y la interpretación geométrica del valor absoluto (a la derecha) de la escuela secundaria…
) y la interpretación geométrica del valor absoluto (a la derecha) de la escuela secundaria…
Pero no nos quejemos, pongámonos a trabajar. En este y en los próximos posts, te mostraré algunos detalles, cuya comprensión facilitará mucho tus estudios universitarios.
Empecemos con…
1. Interpretación geométrica del valor absoluto (como distancia)
Más o menos todos sabemos de qué se trata el valor absoluto. Nadie tiene problemas con el hecho de que:
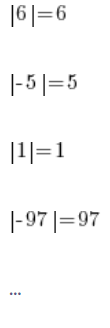
La operación del valor absoluto simplemente devuelve el mismo número, y si es negativo, cambia su signo a positivo.
¿Qué significaría geométricamente? ¿En la línea de números? Pues simplemente la distancia de un número a cero. Por ejemplo, 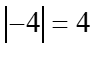 y de hecho, sin duda, la distancia del número
y de hecho, sin duda, la distancia del número ![]() a cero es 4:
a cero es 4:
Seguiremos este camino y entenderemos el valor absoluto precisamente como distancia.
Notemos una cosa más:
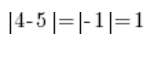
Y que en la línea de números:
…es decir, la distancia entre 4 y 5 es igual al valor numérico de la DIFERENCIA (resta) de 4 y 5, sin importar qué restamos de qué, porque:
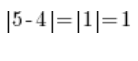
Del mismo modo, si restamos los números 3 y 8 y calculamos el valor absoluto del resultado, obtendremos exactamente la distancia en la línea de números entre los números 3 y 8 (será 5).
Esto también funciona con números negativos, por ejemplo, -1 y 2:
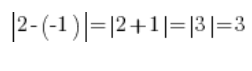
…es decir, precisamente la distancia entre los números -1 y 2:
También puedes jugar un poco con esto tú mismo. Si tienes un libro de texto de la escuela secundaria, te animo encarecidamente a que te sientes una hora con este tema y lo estudies un poco.
Podemos formular una regla general:
El valor absoluto de la diferencia (resta) de dos números: ![]() y
y ![]() es igual a la distancia entre estos números.
es igual a la distancia entre estos números.
¿Cómo podemos descifrar, por ejemplo, tal ecuación:
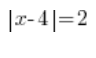
Sabemos que la parte ![]() significa la distancia del desconocido x de 4, y en el lado derecho de la igualdad sabemos que esta distancia debería ser igual a 2.
significa la distancia del desconocido x de 4, y en el lado derecho de la igualdad sabemos que esta distancia debería ser igual a 2.
Entonces, la solución de la ecuación serán los números cuya distancia de 4 es igual a 2, es decir, los números 2 y 6:
Y ahora tomemos esta desigualdad:
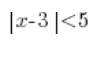
Su lado izquierdo es la distancia x del número 3, y leyendo más obtenemos la información de que esta distancia debería ser menor que 5. Esta vez la solución de esta desigualdad no serán solo dos números, sino muchos más, todos los números cuya distancia de 3 sea menor que 5. En el eje se vería así:
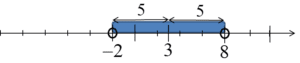
…es decir, serían todos los números desde -2 hasta 8, es decir, el intervalo: ![]() . La distancia de cada uno de estos números de 3 es menor que 5.
. La distancia de cada uno de estos números de 3 es menor que 5.
Este intervalo también se puede llamar un vecindario del punto 3 (un término importante, que se usa mucho en la universidad).
Razonando de la misma manera, puedes averiguar qué números cumplen la desigualdad ![]() …
…
Sin embargo, este no es realmente mi objetivo (ya tuviste esto en la secundaria, ¿verdad 🙂 ?).
Es bueno entender el valor absoluto como distancia, porque aparece en muchas definiciones matemáticas con las que te encontrarás en la universidad. Y entonces es bueno saber de inmediato «de qué va todo esto».
Por ejemplo, tomemos el límite de la sucesión mencionado anteriormente:
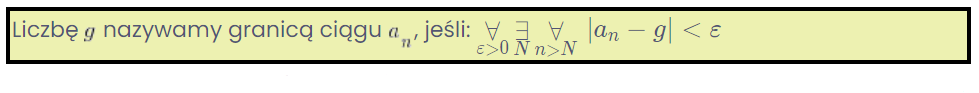
Centrémonos por ahora en el lado derecho de la fórmula. Dejemos los símbolos raros a la izquierda para el próximo post.
¿Cuál lectura llega más al corazón y se entiende mejor:
«el valor absoluto de la diferencia entre ![]() y
y ![]() debe ser menor que
debe ser menor que ![]() »
»
o:
«la distancia entre ![]() y
y ![]() debe ser menor que
debe ser menor que ![]() »
»
?
Formalmente, ambas formas de formular la definición son equivalentes, pero la segunda es más simple y se centra en la esencia, sin distraerse innecesariamente con algunas operaciones aritméticas como la diferencia.
Entender el valor absoluto como distancia te hará mucho más fácil entender muchos teoremas y definiciones matemáticas aparentemente complicadas en la universidad.
¿Qué sigue?
En el próximo post, me ocuparé de estos símbolos raros: ![]() y
y ![]() , para que podamos entender completamente nuestra definición de ejemplo.
, para que podamos entender completamente nuestra definición de ejemplo.