Hay momentos en la vida en los que la región de integración en una integral doble es una elipse….
¿Qué hacemos entonces?
Coordenadas elípticas
Un método elegante para resolverlo es usar las llamadas coordenadas elípticas. Es algo parecido a las coordenadas polares, el mecanismo de funcionamiento es muy similar, solo que sustituyes cosas diferentes por x e y y el Jacobiano es diferente. La interpretación de ‘r’ también es diferente. Entonces, resumiendo, si sabes cómo pasar a coordenadas polares (que generalmente se hace cuando la región de integración es un círculo), también entenderás fácilmente las coordenadas elípticas.
Entonces tenemos la integral: 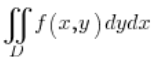 y la región de integración limitada por una elipse con centro en el origen, cuya ecuación es:
y la región de integración limitada por una elipse con centro en el origen, cuya ecuación es: 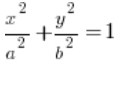 . Asegurémonos de que el lado derecho de la ecuación de la elipse sea 1, ¿de acuerdo? Si por ejemplo es 9, puedes convertirlo fácilmente en 1 dividiendo ambos lados de la ecuación por 9.
. Asegurémonos de que el lado derecho de la ecuación de la elipse sea 1, ¿de acuerdo? Si por ejemplo es 9, puedes convertirlo fácilmente en 1 dividiendo ambos lados de la ecuación por 9.
La región de integración dibujada se ve así:
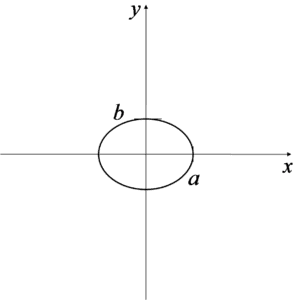
Lo que significan a y b se puede ver en el dibujo. Hay que tener cuidado, porque si en el denominador de la ecuación de la elipse bajo ![]() hay por ejemplo 9, significa que
hay por ejemplo 9, significa que ![]() , por razones obvias, ¿verdad?
, por razones obvias, ¿verdad?
Y ahora, con esta situación «limpia», pasamos a coordenadas elípticas, sustituyendo:
![]()
![]()
Significado de las variables en coordenadas elípticas
El ángulo ![]() significa exactamente lo mismo que en las coordenadas polares, y
significa exactamente lo mismo que en las coordenadas polares, y ![]() significa algo diferente. En problemas básicos con una elipse dada por una ecuación bonita
significa algo diferente. En problemas básicos con una elipse dada por una ecuación bonita 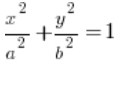 , simplemente asume que
, simplemente asume que ![]() varía de cero a uno (en casos más complicados, sustituye
varía de cero a uno (en casos más complicados, sustituye ![]() y
y ![]() en la ecuación de la elipse y calcula el límite superior de r).
en la ecuación de la elipse y calcula el límite superior de r).
Jacobiano
El Jacobiano en coordenadas elípticas es igual a ![]() .
.
Recordando el Jacobiano, pasamos entonces a la integral en coordenadas elípticas:
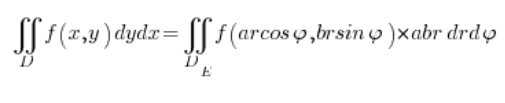
donde las variables ![]() y
y ![]() están limitadas:
están limitadas: ![]() en los límites de cero a uno, y
en los límites de cero a uno, y ![]() dependiendo de si hablamos de toda la elipse, de la mitad, o de, por ejemplo, un cuarto, con diferentes valores de ángulo – igual que en las coordenadas polares.
dependiendo de si hablamos de toda la elipse, de la mitad, o de, por ejemplo, un cuarto, con diferentes valores de ángulo – igual que en las coordenadas polares.
Solo queda tomar y calcular.
Ejemplo
Calcula la integral 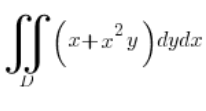 , donde D es la elipse con la ecuación:
, donde D es la elipse con la ecuación: 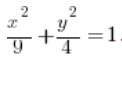 .
.
Siguiendo el esquema anterior, sustituimos:
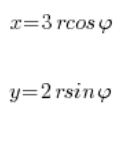
Tomamos la región de integración:
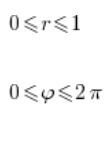
Y calculamos la integral:
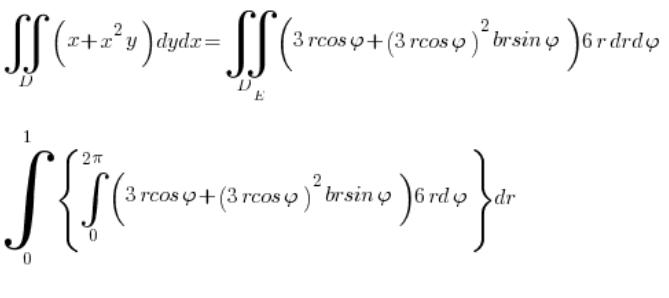
Que por supuesto ya es solo una formalidad 🙂