Formulas for Derivatives
Topic: Theorem on the Derivative of an Inverse Function. Applying the Theorem to Derive Several Derivative Formulas.
Summary
In our lecture, we’re gonna dive into this cool theorem about the derivative of an inverse function. We’ll prove it and see how to use it to figure out a bunch of derivative formulas. Without this theorem, deriving these (like we did directly from definitions in the last lecture) would be, to put it mildly – a tough cookie to crack.
Before tackling the theorem, it’d be great to know what an inverse function is, why the inverse of 
is 
and why we need to limit ourselves in this case to a range of arguments like 
…
Using the theorem to derive formulas is a pretty common task in university-level calculus, so this lecture might just save your academic life one day.
I’m pulling the theorem and proof from Fichtenholz’s book, tweaking it here and there, fixing typos, and making a few alterations.
Theorem on the Derivative of an Inverse Function
If the function 
has an inverse function 
, and at point 
it has a finite and non-zero derivative 
, then at the corresponding point 
the derivative of the inverse function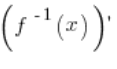 
exists and its value at is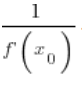 
.
Confused by the string of symbols? At first, it’s very likely, but let’s sink our teeth into this theorem with a couple of simple, concrete examples.
Alright, let’s translate the excerpt into English with a casual and slightly playful tone, including the specialized mathematical terminology:
—
Example 1
If the function
has an inverse function
1. Let’s take the function 
over the interval 
2. Its inverse function exists and is 
– I’m not going to explain why and the reason for this x-interval limitation, sorry…
and at the point
3. Let’s consider the point 
. The derivative of the function exists (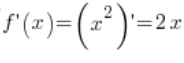
) and at the point its value is non-zero (
).
then at the corresponding point
4. The corresponding point to is the value of the function at point , which is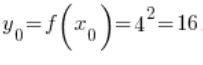 
.
So in our example:
the derivative of the inverse function
5. Indeed, the inverse function is , its derivative is: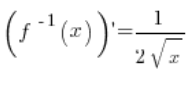 
(from basic derivative formulas) and at the point it definitely exists and is equal to:
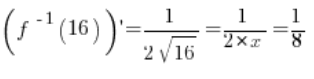
and its value at the point
6. Indeed, the value calculated in point 5.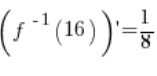 
is equal to:
(
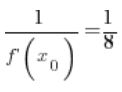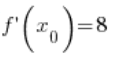– I calculated this in point 3.)
So the Theorem “works” 🙂
Sure, here’s the translation of the specified excerpt from the math blog into English, maintaining a casual and slightly humorous tone:
Example 2
If the function
1. Let’s take the exponential function 
2. Its inverse function exists and is 
– this was in middle school, not explaining again (logarithmic and exponential functions are inverses of each other)
and at the point
3. Let’s take the point 
. The derivative of the function exists (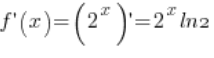
– basic derivative formulas) and at the point its value is non-zero (
).
then at the corresponding point
4. The corresponding point to is the value of the function at point , which is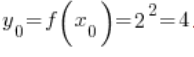 
.
So:
the derivative of the inverse function
5. Indeed, the inverse function is , its derivative is: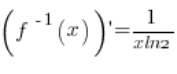 
(from basic derivative formulas). At point , the derivative exists and is equal to:
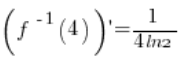
and its value at the point
6. Indeed, calculated at point 5. 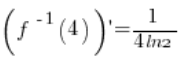is equal to:
(
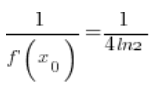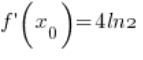– I calculated this at point 3.)
So the Theorem “works” again 🙂
Proof of the Theorem on the Derivative of the Inverse Function
We’ll prove this theorem by referring to the geometric interpretation of the derivative of a function at a point. As we remember, the value of the derivative of a function at a point is the tangent of the slope of the tangent line to the graph of the function at that point.
Graphically, it would look like this:
The value of the derivative at point we defined in previous lectures as the tangent of angle 
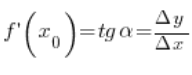
Now let’s notice something interesting: the graph of the inverse function to can be represented on exactly the same graph, only we have to remember to read it “in reverse” – that is, as if we are assigning y values to x arguments (thus, the increment of the arguments of the inverse function is 
, and the increment of its corresponding values is 
):
Notice that the value of the derivative of this inverse function at point equals:
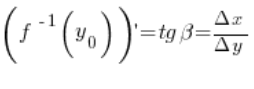
So, we see that the derivative values of the function and its inverse function are the tangents of angles in the same right triangle.
And such tangents of angles in a right triangle (as we remember from high school) are related by the relation:
Thus (after dividing both sides by 
):
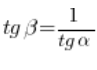
From this follows the conclusion of our theorem, namely:
🙂
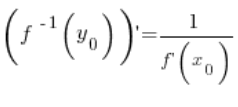
END OF PROOF
Deriving Formulas for Derivatives Using the Theorem on the Derivative of an Inverse Function
Example 3
Let’s derive the formula for the derivative of the function 
.
The formula we need to derive is: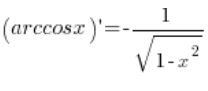 
.
Our function f(x) is the arccosx function. The inverse function to it is 
. The derivative of the inverse function is 
.
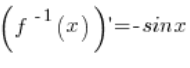According to the theorem on the derivative of an inverse function, the value of the derivative of the inverse function at point is equal to the reciprocal of the value of the derivative of the function at point :
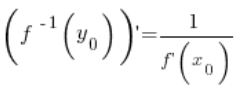
So, at any point :
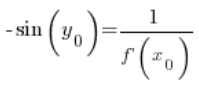
After transforming:
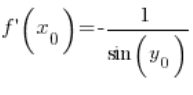
Using the trigonometric identity, we can derive that: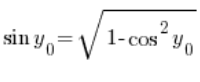 
, so we have:
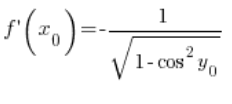
Now, pay attention: is the value of the function at the point , which is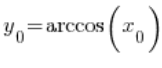 
. Therefore:
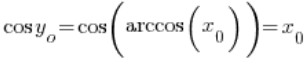– because cosine and arccosine are inverse functions, so we have:
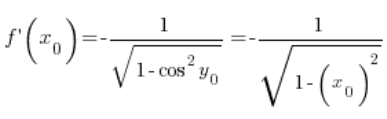at any point (obviously satisfying domain conditions, which I neglected), so our formula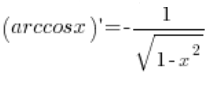 
has been demonstrated in this way.
Example 4
Derive the formula for the derivative of the function 
.
The formula we need to derive is: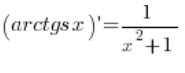 
.
Our function f(x) is the arctgx function. The inverse function to it is 
. The derivative of the inverse function is 
.
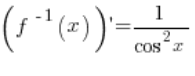According to the theorem on the derivative of an inverse function, the value of the derivative of the inverse function at point is equal to the reciprocal of the value of the derivative of the function at point :
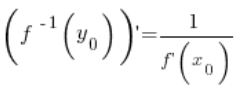
So, at any point :
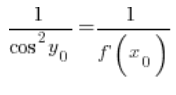
After transforming:
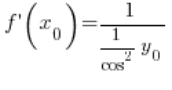
Using the trigonometric identity, we can further transform it:
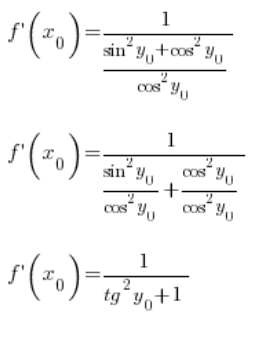
Now, pay attention: is the value of the function at the point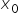 
, which is 
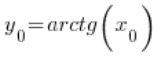. Therefore: 
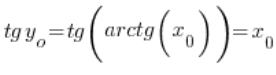– because tangent and arctangent are inverse functions, so we have:
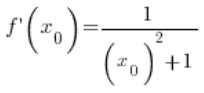at any point (obviously satisfying domain conditions, which I neglected), so our formula 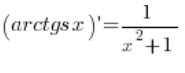has been demonstrated in this way.
THE END
While writing this post, I used…
1. “Differential and Integral Calculus. Volume I.” by G.M. Fichtenholz. Published in 1966.
Click here to see how one can demonstrate the properties of derivatives (next Lecture) –>
Click to return to the main page with lectures on derivatives