Derivatives of Functions Lecture 4
Topic: Testing the Existence of a Derivative – Examples
Summary
This lecture is devoted to several specific problems in which we will prove the existence (or non-existence) of a derivative of a function at a point, using the material from the previous lecture.
Example 1
Check the existence of the derivative of the function f(x) at the point 
:
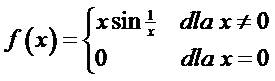
As we saw in the previous lecture, to examine the existence of the derivative of this function at point 0, we need to examine the existence of the left-hand and right-hand derivatives at that point.
We begin with the left-hand derivative:
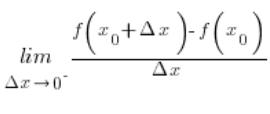
Substituting zero for 
we obtain:
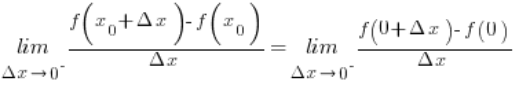
from our formula for the function, and we get:
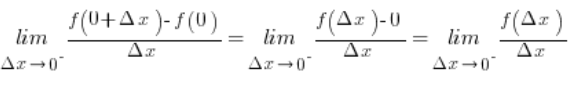
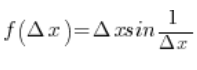from our basic function formula (since \Delta x\ne 0), therefore:
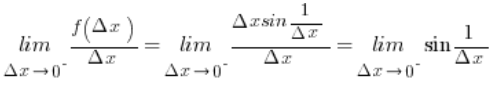
If 
then we have a limit of sine of something diverging to 
, and such a limit does not exist at all (I showed this in one of my blog posts).
Therefore, the left-hand derivative of the function f(x) at the point DOES NOT EXIST.
The entire reasoning could essentially be repeated for the right-hand derivative.
Therefore, the function f(x) does not have at the point either a left-hand or a right-hand derivative. The derivative of this function at this point does not exist (even though it can be shown that the function is continuous at this point).
Example 2
Check the existence of the derivative of the function f(x) at the point :
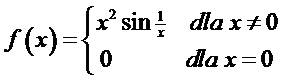
We examine the existence of the one-sided derivatives, starting with the left-hand derivative:
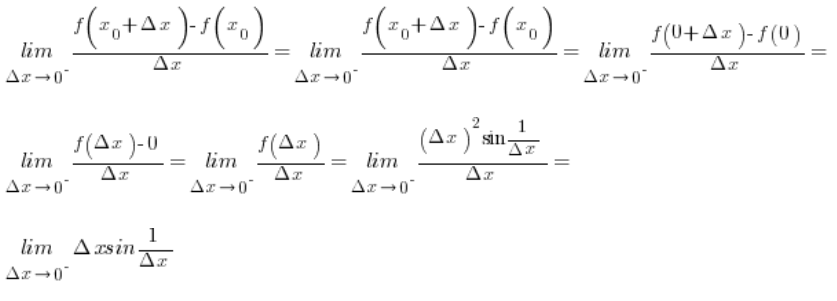
Using the squeeze theorem (see the appropriate post on my blog), one can show that the limit of this function exists and equals zero. Indeed, the inequality holds:
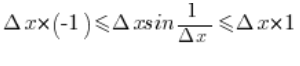
The limit of both the lower bounding function and the upper bounding function equals 0:
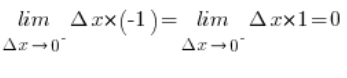
Therefore, by the squeeze theorem:
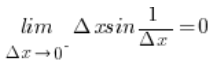
The left-hand derivative therefore exists and equals 0.
The entire reasoning can be repeated for the right-hand derivative, which will also equal 0.
Therefore, the derivative of the function f(x) at point 0 exists and equals 0.
Example 3
Compute the one-sided derivatives of the function 
at the point 
.
We begin with the left-hand derivative:
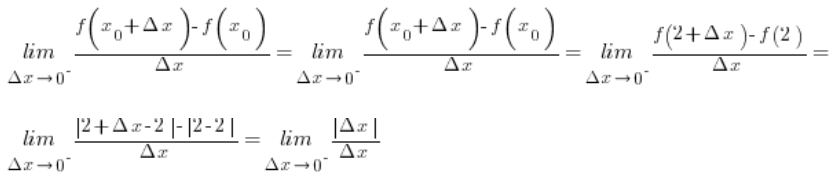
is negative (because 
), therefore:
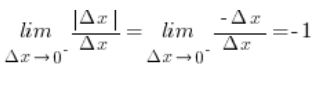
Thus, the left-hand derivative of the function f(x) at point 2 equals -1.
Now we compute the right-hand derivative:
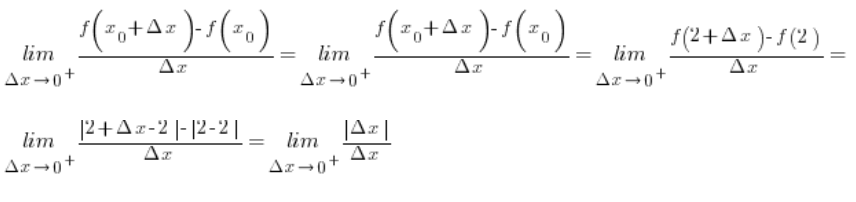
is positive (because 
), therefore:
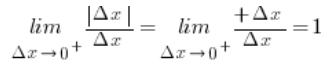
So the right-hand derivative of the function f(x) at point 2 equals 1.
Example 4
Check the existence of the derivative of the function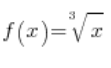 
at the point .
Here let us notice something very interesting. The derivative of the function f(x), computed using formulas, would equal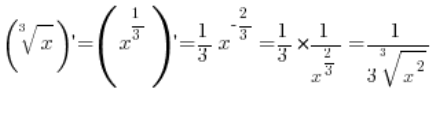 
.
However, the derivative computed using this formula at the point does not exist (this point does not belong to its domain). Therefore, we cannot apply this formula at point and must examine the derivative there using the definition.
We begin with the left-hand derivative:
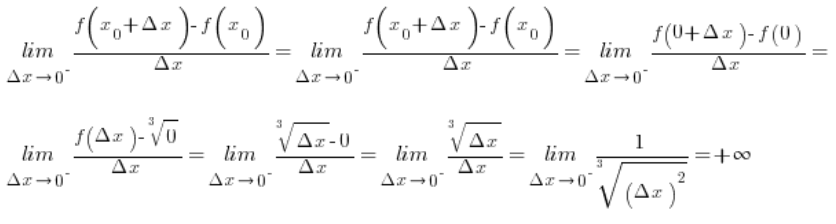
The same result will be obtained when computing the right-hand derivative (in the denominator is always positive because it is squared).
Therefore, the function f(x) has at point 0 an infinite derivative equal to 
.
END
While writing this post I used…
1. “Differential and Integral Calculus. Volume I.” G.M. Fichtenholz. Ed. 1966.
Click to recall how to compute one-sided derivatives of functions (previous Lecture) <–
Click to proceed to formulas for derivatives (next Lecture) –>