Triple Integral Calculator (OUTDATED). Invitation to the New Version.
Krystian Karczyński
Founder and General Manager of eTrapez.
Graduate of Mathematics at Poznan University of Technology. Mathematics tutor with many years of experience. Creator of the first eTrapez Courses, which have gained immense popularity among students nationwide.
He lives in Szczecin, Poland. He enjoys walks in the woods, beaches and kayaking.
Announcement
Unfortunately, after over 13 years of providing a free triple integral calculator, I had to “shut it down”.
The calculator was a simple “widget” for the WolframAlpha site. Some time ago, WolframAlpha changed its policy regarding widgets. Among other changes: they no longer compute “on-site” but redirect the user to the WolframAlpha site.
I apologize for the inconvenience to all the former users of the Triple Integral Calculator.
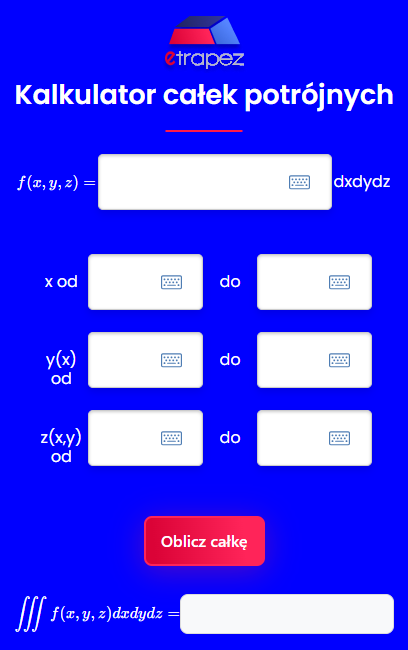
New Triple Integral Calculator
I also invite you to try the new triple integral calculator, which I created using open-source technology. You can access it and other interactive tools with a subscription for only 5.99 PLN/month (or cheaper with multi-month options) at:
And here’s what the calculator looks like:
Best regards and good luck!
Krystian Karczyński
Are you looking for college or high school math tutoring? Or maybe you need a course that will prepare you for the final exam?
We are "eTrapez" team. We teach mathematics in a clear, simple and very precise way - we will reach even the most knowledge-resistant students.
We have created video courses translated in an easy, understandable language, which can be downloaded to your computer, tablet or phone. You turn on the video, watch and listen, just like during private lessons. At any time of the day or night.