The Volume of an Ellipsoid (But Not a Rotational One, Just a Wild Type) Calculated by a Definite Integral

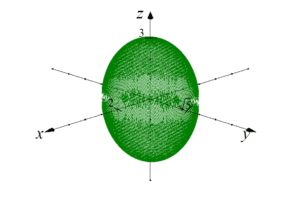
Let’s say we need to calculate the volume of an ellipsoid:

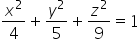
This ellipsoid intersects the x, y, z axes at coordinates 2, and 3, respectively (the general equation of the ellipsoid is: 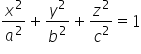, where a, b, c are the coordinates of the intersections).

This is not a rotational ellipsoid, not formed by rotating any curve around any axis, so we can’t use the standard formula for the volume of a rotational solid:

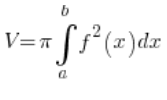
We need to figure out another way.

1. Choose any point M(z) at the center of the ellipsoid and on the OZ axis.

A plane passing through this point and perpendicular to the OZ axis „cuts” out a certain ellipse from the ellipsoid:

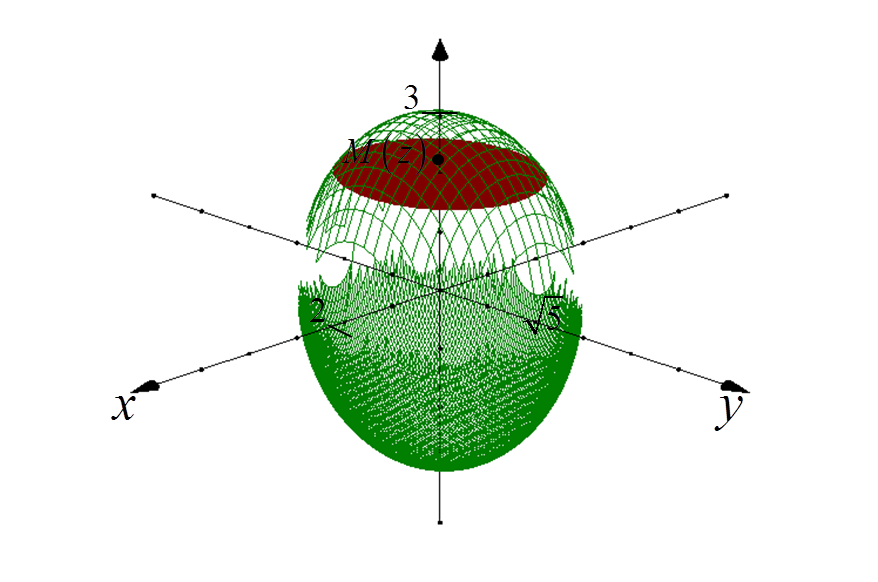
2. Determine the equation of the „cut-out” ellipse projection on the XY plane

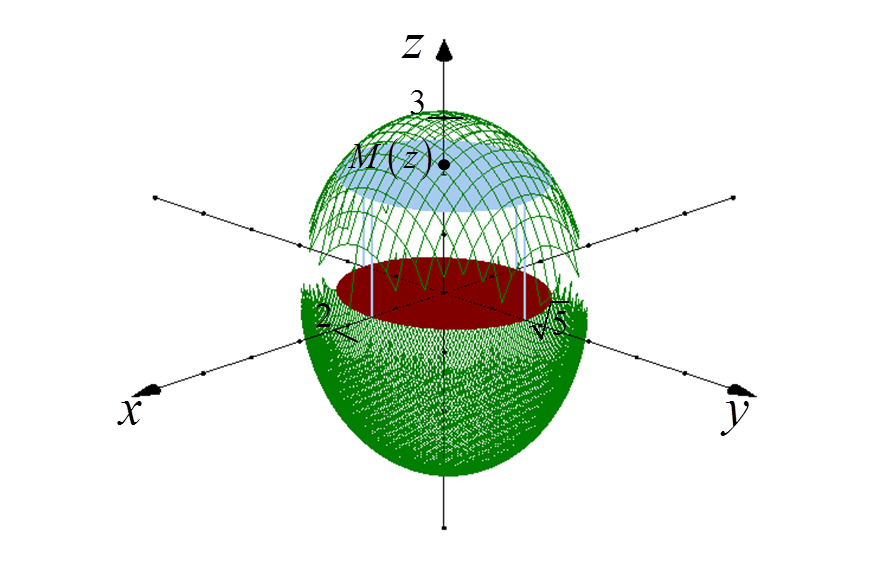
We determine the equation of this ellipse, for a fixed 'z’ (treating 'z’ as a constant) from the general equation of the ellipsoid:

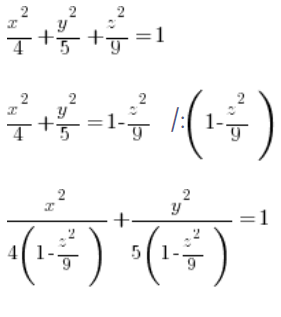
You can see that our 'a’ and 'b’ from the general equation of the ellipsoid (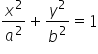) are:

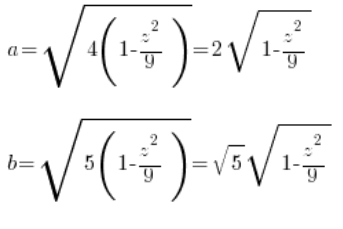
4. Calculate the area of this section as a function of 'z’

The area of this ellipse depends on the chosen point 'z’, so it will be a function of 'z’. We can calculate it either using the ready formula for the area of an ellipse ():

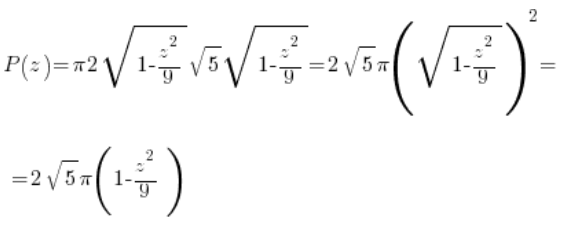
Or by laboriously calculating the appropriate definite integral (using, of course, the parametric form of the ellipse and the formula for the area of a region in parametric form):

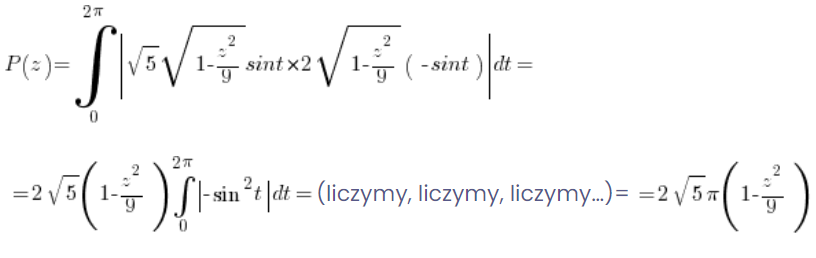
5. Calculate the volume of the solid using the cross-sectional areas

Now comes the tricky part. The volume of the solid is equal to – this sounds a bit awkward – the „sum” (i.e., the integral) of all the cross-sections, which in general is:

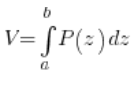
where is the function of the cross-sectional areas of the solid with a plane perpendicular to the OZ axis, and 'a’ and 'b’ are the bounds within which 'z’ varies.

So for us:

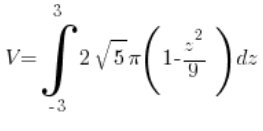= (calculate, calculate, calculate…) =

This matches the general formula for the ellipsoid ().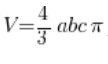

THE END

It’s worth remembering this general scheme, and most importantly, that the volume of more complex, non-rotational solids can be calculated by integrating the function of their cross-sectional areas.