Currently Empty: zł0.00
Krystian Karczyński- 29 April 2024
- Comment 0
The Limit of a Sequence with the Number e… Is It Really?
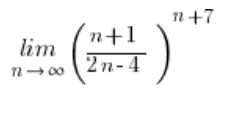
If we’ve solved some problems on sequence limits, we might fall into a bit of a routine. We might approach this limit like we do with limits involving the number e in the result: subtract and add 4 in the numerator, split it into two fractions, and so on. But by doing so, we encounter a slight problem…
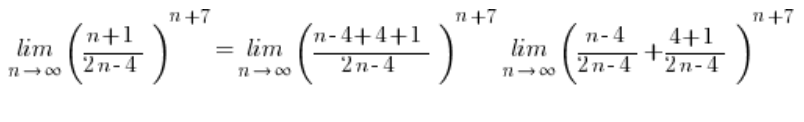
This time, the first fraction doesn’t simplify at all and doesn’t give a one!
Teachers often don’t elaborate on this, but we apply limits involving the number e when there’s an indeterminate form 
, and in our example:
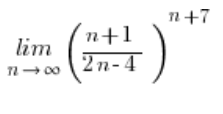
Second part:
The quotient of polynomials raised to a power doesn’t approach 1 at all, but 
, as we can see by extracting the highest powers outside the parentheses:
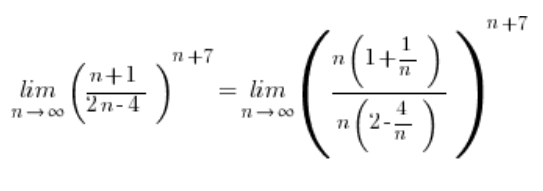
So, we get a situation of 
, and this sequence limit from the appropriate formula is 0:
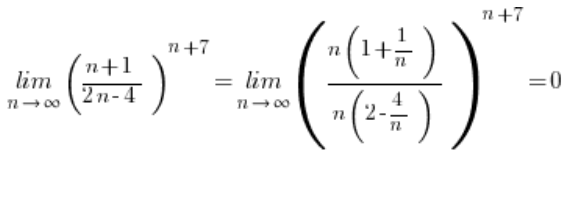
The Problem with These Kinds of Limits
Before you tackle a sequence limit with formulas involving the number e, consider if the expression raised to a power tends to 1 at all. In the case of dividing a polynomial by another polynomial, this can be easily checked without calculations. This division will tend to 1 if the highest powers of the polynomials are the same and the coefficients in front of them are the same too. In that case, you can apply the method of the sequence limit involving the number e. If not, you probably need to extract the highest power outside.
Judge for Yourself, at a Glance
Finally, an exercise. Look at the limits below and judge “at a glance” which ones need to be solved by the limit involving the number e method and which ones by extracting the highest power:
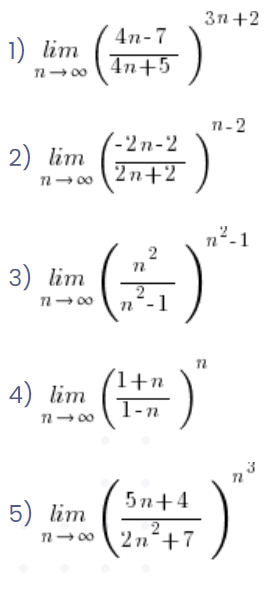
… and they all look so similar… 🙂
