Proving that sinx does not reach a limit as x approaches infinity

Krystian Karczyński

Founder and General Manager of eTrapez.

Graduate of Mathematics at Poznan University of Technology. Mathematics tutor with many years of experience. Creator of the first eTrapez Courses, which have gained immense popularity among students nationwide.

He lives in Szczecin, Poland. He enjoys walks in the woods, beaches and kayaking.

We have the limit of the function:

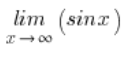
We intuitively feel that the above limit does not exist. x’s are getting bigger and bigger, and the sine values ​​are constantly fluctuating between -1 and 1.

Formal proof

But how can we formally demonstrate and prove this?

From the definition of the limit of a function as x approaches infinity , we know that the limit exists if for each sequence of arguments of the function diverging in the corresponding sequence of function values ​​converges to the same number (then this number is the limit).

To show that such a limit does not exist, it is enough to take two random sequences of arguments diverging in and show that the corresponding sequences of values ​​converge to two different numbers.

We know that the sine function is periodic, so these can be, for example, the sequences:

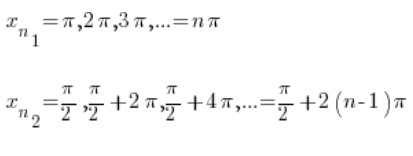
Of course, both sequences diverge to infinity at

Now let’s look at the corresponding sequences of function values : :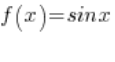

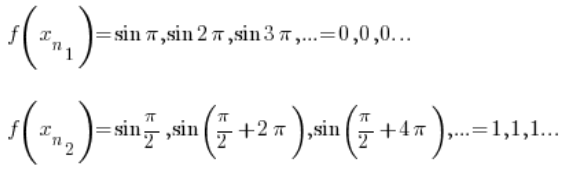
Of course, the first sequence converges to 0, and the second sequence converges to 1.

This is enough to prove that the limit of the function:

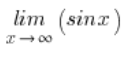
does not exist.