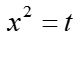In indefinite rational integrals, as we know, we often need to factor the denominator of the integrand and further decompose it into simple fractions.
However, factorization itself can often be tricky.
Typical situations
For simple situations like:
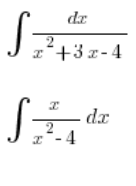
We can handle it:
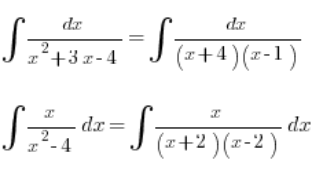
If the denominator is a properly “arranged” third-degree polynomial, we can still manage:
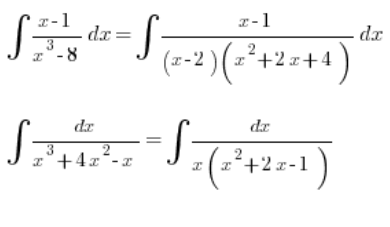
Denominator with an unfriendly third-degree polynomial
The problem starts when the denominator has a more “unfriendly” third-degree polynomial to factorize, for example:
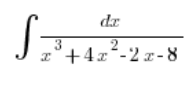
Deep breath.
Control the panic.
Such things (factoring this type of polynomial) were done in high school and at the basic level.
Just need a clever trick:
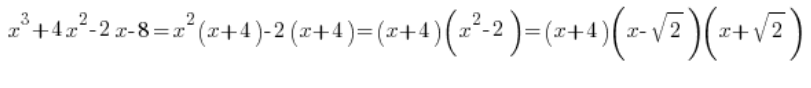
Remember? Of course you do…
So we can factorize the polynomial in the denominator:
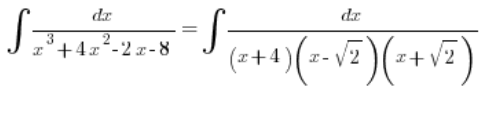
And then cheerfully decompose it into three simple fractions, as the rules tell us.
Even more difficult factorization
And what about such a situation? Remember from high school (this is more of an extended scope)?
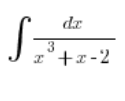
Here it was a bit worse. The middle term needed to be split into two:
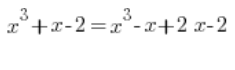
And then proceed as usual:
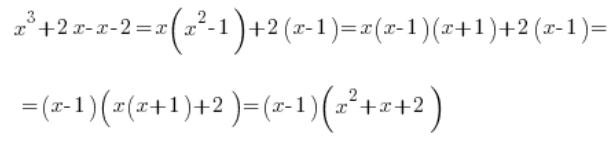
So the integral should be written as:
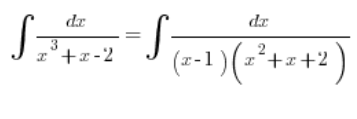
And continue calculating calmly.
Methods of factorizing the denominator in rational integrals
Generally, remember in rational integrals that if factorizing the polynomial is needed, all high school tricks are allowed, and they might include, for example:
- Factorizing some fourth-degree polynomials by substitution

- Blindly searching for a root and dividing the polynomial to reduce its degree
Of course, we are now only talking about the more difficult indefinite rational integrals, which in many (most?) universities are not even introduced!