Euler Substitutions of the Third Kind – Summary

---

Euler Substitutions of the First, Second, and Third Kind – More Than Enough

In previous posts, I showed how to use Euler substitutions in integrals of the type:

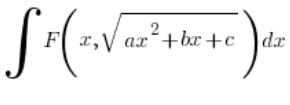
• Euler Substitutions of the First Kind (when a>0)
• Euler Substitutions of the Second Kind (when c>0)

In this post, we’ll deal with the third and final type of Euler substitution, which we can use when in the integral:

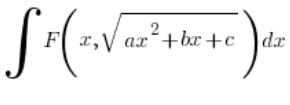
the quadratic polynomial , has two distinct roots , meaning when its 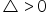, meaning it can be written in factored form: .

But before we get to the practical stuff, let’s notice that these three cases:

• First kind, when a>0
• Second kind, when c>0
• Third kind when there are two distinct roots

will allow us to solve any integral of the type:

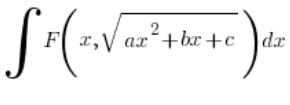
In fact, even just the first and third kinds are enough.

Why?

The case when can be ignored because the quadratic polynomial simply becomes a linear form , which we can solve using simpler substitutions than Euler’s.

But what about the case when a<0 (doesn’t fit the first kind) and the quadratic polynomial has one or no roots at all (doesn’t fit the third kind)?

Then its graph would look like this (remember from middle school – arms down):

or, if it had no roots at all, like this:

What’s the takeaway? That in both cases the quadratic polynomial would take negative values (except for at most one point), and I remind you, we’re calculating the integral:

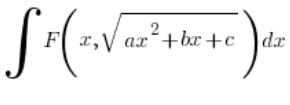
Meaning, in the integrand, the quadratic polynomial is under the square root, and you can’t take the square root of negative values (we’re playing with real numbers, of course). So the domain of such a function would be at most one point, which is pointless, and we certainly won’t get such an example. Unless the professor is really sleep-deprived when making the test.

So, the case when a<0 and the quadratic polynomial has no two roots can be ignored, and it’s now clear that the first and third kinds of Euler substitutions fit any integral of the type:

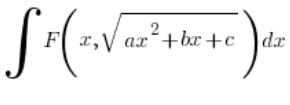
So, let’s get to the third kind of Euler substitution.

Euler Substitutions of the Third Kind

We have an integral:

,

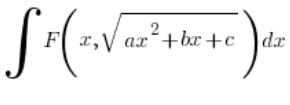where has , meaning it can be written as:

,

where are its roots.

The substitution we use here is:

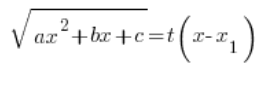
We square both sides of this substitution, write the quadratic on the left in factored form (we know we can), divide both sides by , and proceed as in the previous types of substitutions, determining in sequence:

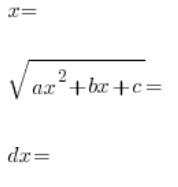
Finally, we substitute everything into the original integral and end up with a usually tedious rational integral.

Let’s get started.

Example

Our (meaning a<0, so we won’t use the first kind of substitution), our (meaning c<0, so we won’t use the second kind of substitution), but our , meaning we can use the third kind of substitution.

We first calculate :

We use the third kind of Euler substitution:

We square both sides:

We write the quadratic on the left in factored form (remember here!!!):

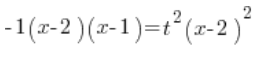
We divide both sides by :

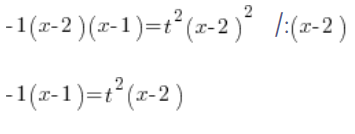
We determine :

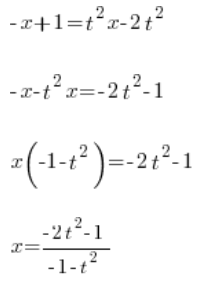
We have determined using variable . Now let’s determine .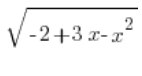

Returning to our first substitution, we have:

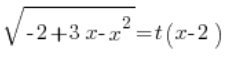
We substitute the determined 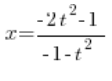, and we get:

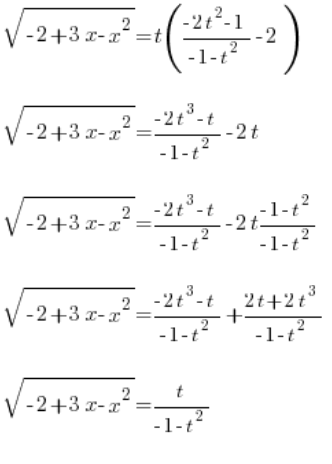
We have nicely determined 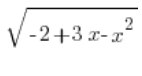. Now only remains, which we will calculate by finding the derivative of :

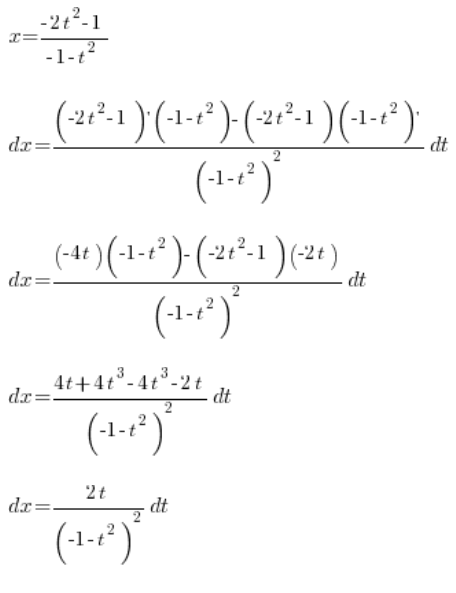
So we have determined:

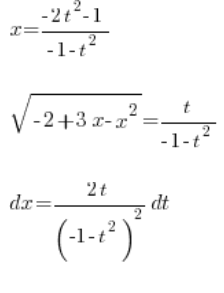
, everything using variable . We put this into the integral:

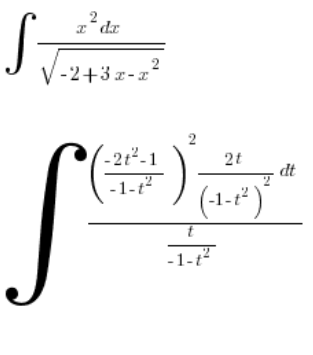
We simplify:

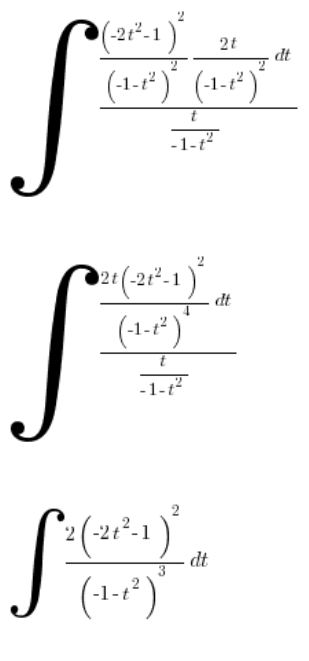
As expected, we get a really complex rational integral, which I won’t calculate.

Finally, it’s worth noting that…

Note on Euler Substitutions

We have an integral:

  ,

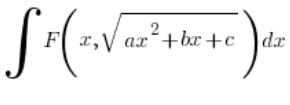where:

• First kind, when a>0
• Second kind, when c>0
• Third kind when there are two distinct roots

It’s obvious that it can often be solved using one of the two Euler substitutions, or even any of them (when a>0, c>0 and at the same time ).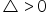

No problem, although for ease of calculation I would recommend using the first kind first, if that doesn’t work, then the second, and if that doesn’t work, then finally the third.

That’s all on using Euler substitutions, I hope it helps you in your studies, and as always, feel free to comment below the post.