Complex Polynomial Equations Reducible to Quadratic Equations

---

Reducing Some Fourth-Degree Equations to Quadratic Equations

Many fourth-degree polynomial equations can be transformed into quadratic equations using a well-known high school trick described here:

Reducing to a Quadratic Equation

This works, of course, and very much so for polynomials in complex numbers.

To remind you, what we do is having the equation:

{{z}^{4}}+3{{z}^{2}}+2=0

We substitute: {{z}^{2}}=t

And we get a quadratic equation:

{{t}^{2}}+3{t}+2=0

Then we solve it using the usual delta and so on, we get solutions , remembering that we form two next equations from them:

or

We solve them and we have four solutions: .

Reducing Some Higher-Degree Equations to Quadratic Equations

Absolutely nothing stands in the way of extending this method to equations of degrees higher than 4 (if, of course, they can be reduced to quadratic equations by substitution).

So we have:

2{{z}^{6}}-5{{z}^{3}}+4=0

We can also notice that it is equivalent to:

2{( {z}^{3})^{2}}-5{{z}^{3}}+4=0

And after substituting:

We get a quadratic equation:

2{{t}^{2}}-5t+4=0

In the equation:

{{x}^{10}}-3{{x}^{5}}+1=0

After substituting:

We have:

{{t}^{2}}-3t+1=0

And so on, and so on…

Example

Let’s take the equation:

z^6+(1-i)z^3-i=0

We substitute z^2=t and we have:

t^2+(1-i)t-i=0

Then we calculate:

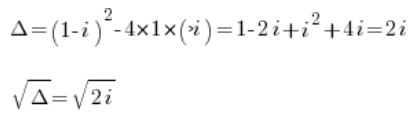
We calculate these roots using the methods known from complex numbers (shown for example in my Course).

We have or

That is:

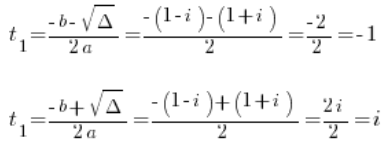
Remembering that these are not solutions yet, because z^3=t

So we have to solve the equations:

z^3=-1

And:

z^3=i

We transform them into:

and

And calculating again using the known methods, we have three roots from the first equation:

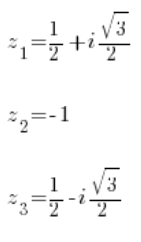
And three roots from the second equation:

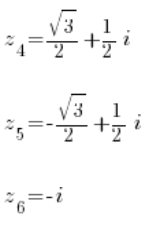
Solved 🙂