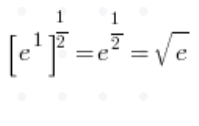No products in the cart.
Krystian Karczyński- 18 June 2024
- Komentarz 0
Typical Sequence Limits with a Formula for the Number e
Traditional problems on sequence limits with a formula for the number e quite “naturally” lead to the formula (I show how to do this in my Course):
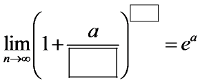But what if, instead of such a neat fraction, we have something like this in the parentheses:
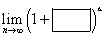If the rectangle in the parentheses tends to zero, and the triangle in the exponent tends to infinity, we have an indeterminate form 
– exactly the type where we use the formula with the number ‘e’ in the result. What to do?
Well, let’s remember that any expression can be represented as dividing one by the reciprocal of that expression 🙂
For example, the simple, polite number 2 can be written as:
So, any expression can be “forcibly” made into a fraction if really necessary.
Example of an Unconventional Limit with a Formula for the Number e
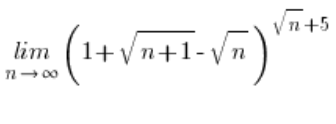
First, it should be shown that the expression 
tends to zero. You do this by calculating the limit:
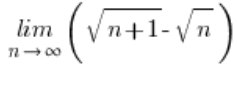– the result will indeed be zero (you can use the method of multiplying by the conjugate).
Now, replace:
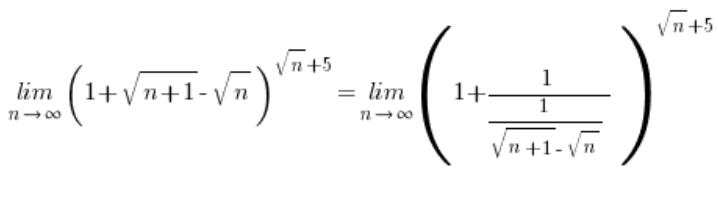
… and continue according to the known scheme:
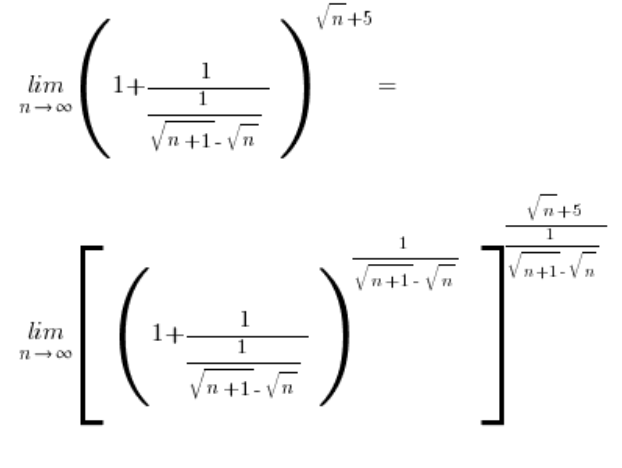
The limit in the big square bracket is: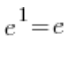 
– according to the basic formula, only the final step remains with:
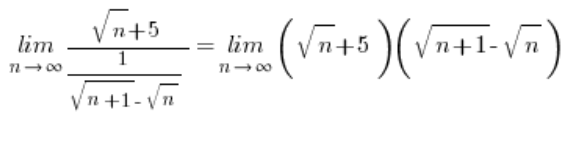
… which, after applying multiplication by the conjugate, will end up with the result 
.
Thus, the whole limit is equal to:
