Asymptotes Lecture 2
Topic: Oblique Asymptotes – Definition
Summary
In this lecture we define what oblique asymptotes of a function are (as a certain type of improper limit of a function).
We will need:
- the definition of the improper limit of a function as
from the previous Lecture (Asymptotes Lecture 1)
What is an asymptote as ? Intuitive explanation
In the previous lecture we introduced horizontal asymptotes – they were horizontal lines that the graph of a function approached as its arguments (x) diverged to infinity. We could say that the graph had a horizontal asymptote when, for arguments of the function diverging to 
(or to 
), the corresponding function values converged to some number g, that is, for 
.
On the graph, this could look for example like this:
So we have two things: arguments x diverging to infinity and the graph of the function approaching another curve. In our case, actually a line. A horizontal one. 🙂
However, there is no need to restrict ourselves only to horizontal lines when it comes to the curve that the graph of the function f(x) approaches. In fact, it may be any line (not necessarily horizontal), or even any other curve. The important condition is that the graphs “approach” this curve for arguments diverging to infinity. In other words, for arguments diverging to plus/minus infinity, the distance between the values of the function and the values of this curve should converge to zero.
Remembering that the distance between two values can be expressed as the absolute value of their difference, symbolically, if we denote the function by f(x) and the curve by d, the condition for the existence of an asymptote of the function as will be:
The conclusion is that there can be only two such asymptotes: as 
and as 
.
Oblique asymptotes as a special case of asymptotes as .
Since asymptotes as can be any curve, they can also be a line, right? 🙂
And these are what we call oblique asymptotes. It could look for example like this:
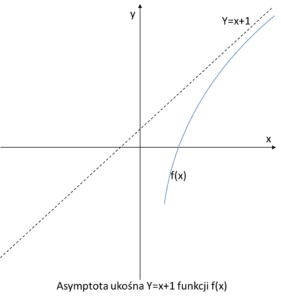
The general condition for the existence of an asymptote is, let us recall:
… where d is the graph of the curve that is the asymptote. If we agree that this curve is a line (sounds funny, right?), then its general equation (as we know from school) is: 
. We can substitute this for d, obtaining:
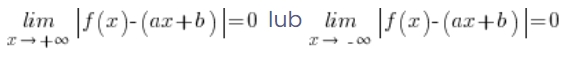
That is:
The absolute value equals zero if and only if it is taken of zero (or – as in our case – something tending to zero), therefore:
After dividing both sides of the equation by x, we obtain:
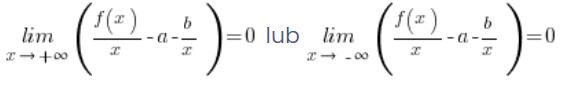
The expressions 
in these limits tend to zero (a constant divided by infinity), therefore the above equations will be satisfied when:
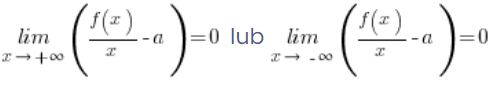
And this, in turn, will be satisfied when:
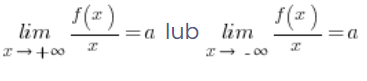
On the other hand, it is immediately clear that the original condition:
is satisfied when (I moved b to the right-hand side):
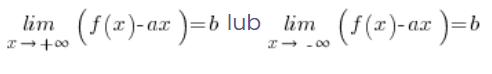
In this way, we have derived the necessary conditions for the existence of an oblique asymptote. Summarizing:
Conditions for the existence of oblique asymptotes
The function f(x) has the oblique asymptote as when:
1. 
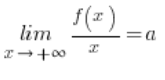
2. 
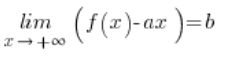
The function f(x) has the oblique asymptote as when:
1.
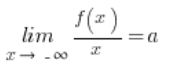
2. 
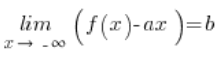
Click here to review vertical and horizontal asymptotes (previous Lecture) <–