Hyperbolic Functions for Help

Lecture

Topic: Hyperbolic functions

Hyperbolic functions are functions “similar” to trigonometric functions.

“Similar” means having “similar”:

• names
• properties
• derivatives

However, it should be understood that “similar” does not mean “same”. Hyperbolic functions are completely new functions to learn.

Where are they useful? In some issues, especially at technical universities, their use makes things easier.

For example, in indefinite integrals the elementary formula:

16.\quad \int{\frac{dx} {\sqrt{{{x} ^{2} }+q}}=\ln \left| x+\sqrt{{{x} ^{2} }+q} \right|+C}

…can also be expressed as:

\int{\frac{dx}{\sqrt{{{x}^{2}}+{{a}^{2}}}}}={{\sinh }^{-1}}\left( \frac{x}{a} \right)+C

This version of the formula is also used by Wolframalpha , which often confuses students (when they check their result with Wolframalpha and see some hyperbolic sines there, they automatically assume that they calculated something wrong).

In this article, I will show you what hyperbolic functions are, what properties and derivatives they have, and how they are similar to the trigonometric functions you already know.

I will also show you how to apply them to indefinite integrals and how they can help do the math tasks.

Hyperbolic function – what are they anyway?

Hyperbolic functions are functions whose values ​​are created by various combinations with the values ​​of the e^x function, specifically:

Hyperbolic sine : \sinh x=\frac{{{e} ^{x} }-{{e} ^{-x} }}{2}

Hyperbolic cosine: \cosh x=\frac{{{e} ^{x} }+{{e} ^{-x} }}{2}

Hyperbolic tangent: tghx=\frac{\sinh x}{\cosh x}=\frac{{{e}^{x}}-{{e}^{-x}}}{{{e}^{x}}+{{e}^{-x}}}

Hyperbolic cotangent: ctghx=\frac{\cosh x}{\sinh x}=\frac{{{e}^{x}}+{{e}^{-x}}}{{{e}^{x}}-{{e}^{-x}}}

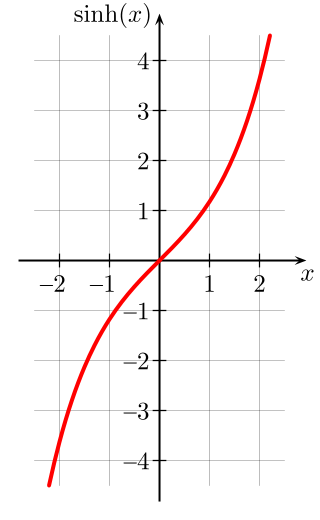
And that’s it. That’s the whole definition. The hyperbolic sine function simply has this formula and that’s it. To get a better feel for the function, I invite you to play a bit with its plot. Substitute a few numbers into the formula for x, calculate the values ​​and mark the dots on the plot.

For a hyperbolic sine, for example, the dots should form a plot like this:

You can also draw plots of other functions or find them on Wikipedia .

Properties of hyperbolic functions

Why exactly would someone call this: \frac{{{e} ^{x} }-{{e} ^{-x} }}{2}– “sine” at all? Where does this word come from? Because there isn’t much trigonometry in this…

Well, because “this thing” has very similar properties to the trigonometric function “sine”. In general, this is very interesting in mathematics. Finding unusual similarities and analogies between objects – it would seem – from completely different fairy tales.

So this occurs:

{{\cosh }^{2} }x-{{\sinh }^2} x=1 (similar but not the same, to trigonometric identity)

\cosh 2x={{\cosh }^{2} }x+{{\sinh }^{2} }x (similar to the formula for cos2x)

\sinh 2x=2\sinh x\cosh x (identical to the formula for sin2x)

It is easy to proove these properties, just substitute the expressions from the definitions and count them. Let’s take for example up the first one:

{{\cosh }^{2}}x-{{\sinh }^{2}}x={{\left( \frac{{{e}^{x}}+{{e}^{-x}}}{2} \right)}^{2}}-{{\left( \frac{{{e}^{x}}-{{e}^{-x}}}{2} \right)}^{2}}=\frac{{{e}^{2x}}+2{{e}^{x}}{{e}^{-x}}+{{e}^{-2x}}}{4}-\frac{{{e}^{2x}}-2{{e}^{x}}{{e}^{-x}}+{{e}^{-2x}}}{4}= =\frac{{{e}^{2x}}+2{{e}^{x-x}}+{{e}^{-2x}}-\left( {{e}^{2x}}-2{{e}^{x-x}}+{{e}^{-2x}} \right)}{4}=\frac{{{e}^{2x}}+2{{e}^{0}}+{{e}^{-2x}}-{{e}^{2x}}+2{{e}^{0}}-{{e}^{-2x}}}{4}=\frac{4}{4}=1

Hyperbolic and trigonometric functions are also similar in complex numbers, but I will not write about it here (you can read about it on Wikipedia ).

Derivatives of hyperbolic functions

What are the derivatives of hyperbolic functions? Again – similar to derivatives of trygonometric functions.

For example, let’s calculate the derivative of the hyperbolic sine:

{{\left( \sinh x \right)}^{\prime }}={{\left( \frac{{{e} ^{x} }-{{e} ^{-x} }}{2} \right)}^{\prime }}=\frac{1}{2}{{\left( {{e} ^{x} }-{{e} ^{-x} } \right)}^{\prime }}=\frac{1}{2}\left[ {{\left( {{e} ^{x} } \right)}^{\prime }}-{{\left( {{e} ^{-x} } \right)}^{\prime }} \right]=\frac{1}{2}\left( {{e}^{x}}+{{e}^{-x}} \right)=\frac{{{e}^{x}}+{{e}^{-x}}}{2}=\cosh x

And for all functions we would get:

{{\left( \sinh x \right)}^{\prime }}=\cosh x (same as in trigonometrics)

{{\left( \cosh x \right)}^{\prime }}=\sinh x (same as in trigonometry, only different sign)

{{\left( tghx \right)}^{\prime }}=\frac{1} {{{\cosh }^{2} }x} (same as in trigonometrics)

{{\left( ctghx \right)}^{\prime }}=\frac{-1} {{{\sinh }^{2} }x} (same as in trigonometrics)

Inverse hyperbolic functions – let’s make it even more confusing

I will now determine the inverse function of the hyperbolic sine.

Let’s this function:

y=\frac{{{e} ^{x} }-{{e} ^{-x} }}{2}

This is an expression in which ‘y’ is function of ‘x’. When looking for an inverse function, you need to determine ‘x’ using ‘y’.

Sometimes it’s easy, sometimes a little less easy. This would be ‘a little less’ case.

I’m going in:

y=\frac{{{e} ^{x} }-{{e} ^{-x} }}{2}

y=\frac{{{e} ^{x} }-{{e} ^{-x} }}{2} /\cdot 2

2y={{e} ^{x} }-{{e} ^{-x} }

2y={{e} ^{x} }-\frac{1} {{{e} ^{x} }} /\cdot {{e} ^{x} }

2y{{e} ^{x} }={{\left( {{e} ^{x} } \right)}^{2} }-1.

-{{\left( {{e} ^{x} } \right)}^{2} }+2y{{e} ^{x} }+1=0.

t={{e} ^{x} }.

-{{t} ^{2} }+2yt+1=0.

\Delta ={{\left( 2y \right)}^{2} }-4\cdot \left( -1 \right)\cdot 1=4{{y} ^{2} }+4.

{{t}_{1}}=\frac{-2y-\sqrt{4{{y}^{2}}+4}}{2\cdot \left( -1 \right)}=\frac{-2y-\sqrt{4\left( {{y}^{2}}+1 \right)}}{-2}=\frac{-2y-2\sqrt{{{y}^{2}}+1}}{2}=\frac{2\left( -y-\sqrt{{{y}^{2}}+1} \right)}{-2}=y+\sqrt{{{y}^{2}}+1}.

{{t}_{2}}=\frac{-2y+\sqrt{4{{y}^{2}}+4}}{2\cdot \left( -1 \right)}=\frac{-2y+\sqrt{4\left( {{y}^{2}}+1 \right)}}{-2}=\frac{-2y+2\sqrt{{{y}^{2}}+1}}{-2}=\frac{2\left( -y+\sqrt{{{y}^{2}}+1} \right)}{-2}=y-\sqrt{{{y}^{2}}+1}.

That is, remembering that t={{e} ^{x} }

{{e}^{x}}=y+\sqrt{{{y}^{2}}+1}\quad \vee \quad {{e}^{x}}=y-\sqrt{{{y}^{2}}+1}

I reject the later because the expression y-\sqrt{{{y} ^{2} }+1} is always negative and e^x cannot be negative.

So I am left with only:

{{e} ^{x} }=y+\sqrt{{{y} ^{2} }+1}

Now I “apply logarithm” on both sides using natural logarithm:

{{e} ^{x} }=y+\sqrt{{{y} ^{2} }+1} /\ln\ldots

\ln {{e} ^{x} }=\ln \left( y+\sqrt{{{y} ^{2} }+1} \right).

x\ln e=\ln \left( y+\sqrt{{{y} ^{2} }+1} \right).

x=\ln \left( y+\sqrt{{{y} ^{2} }+1} \right)

And I’ve got x!

Therefore, the inverse function of the hyperbolic sine: \frac{{{e} ^{x} }-{{e} ^{-x} }}{2} is function: \ln \left( x+\sqrt{{{x} ^{2} }+1} \right).

We can denote it this way:

{{\sinh }^{-1} }x=\ln \left( x+\sqrt{{{x} ^{2} }+1} \right)

Which is obviously associated with the inverse function notation…

Or we can denote it this way:

arsinh x=\ln \left( x+\sqrt{{{x} ^{2} }+1} \right)

Which refers to functions inverse to trigonometric functions (arcsinx inverse to sinx).

The first denotation is of course better because it is not misleading.

In Poland, inverse hyperbolic functions are called “area functions” for example: “area hyperbolic sine”. I also came across the expressions “sine and hyperbolic”, but only from students, because I didn’t read find it anywhere in literature.

All formulas for inverse hyperbolic functions are:

arsinh x=\ln \left( x+\sqrt{{{x} ^{2} }+1} \right).

arcosh x=\ln \left( x\pm \sqrt{{{x} ^{2} }-1} \right).

artghx=\frac{1}{2} \ln \frac{1+x}{1-x}.

arctghx=\frac{1}{2} \ln \frac{x+1}{x-1}.

One of those functions we can meet in elementary integrals formulas I mentioned at the begining:

\int{\frac{dx}{\sqrt{{{x}^{2}}+{{a}^{2}}}}}={{\sinh }^{-1}}\left( \frac{x}{a} \right)+C

You can read more about “area functions” (i.e. inverse hyperbolic functions), their graphs, derivatives, etc. on Wikipedia .

Applications of hyperbolic functions and their inverses

Hyperbolic functions, thanks to their neat properties and derivatives, are useful in many places in calculus. The first (and honestly, often the last) of cases for many students are some formulas for indefinite integrals.

For example, let’s say we want to evaluate the integral \int{\frac{dx} {\sqrt{{{x} ^{2} }+7}}} and let’s assume we do NOT know the formula:

\int{\frac{dx} {\sqrt{{{x} ^{2} }+q}}}=\ln \left| x+\sqrt{{{x} ^{2} }+q} \right|+C

In that case, we could solve the integral by substituting a hyperbolic function \sqrt{7} \sinh t=x (I showed the substitution method in my Course ). Further differentiating both sides I would have: \sqrt{7} \cosh tdt=dx. Furthermore I need to denote \sqrt{{{x} ^{2} }+7}:

\sqrt{{{x} ^{2} }+7}=\sqrt{{{\left( \sqrt{7} \sinh t \right)}^{2} }+7}.

\sqrt{{{x} ^{2} }+7}=\sqrt{7{{\sinh }^{2} }t+7}.

\sqrt{{{x} ^{2} }+7}=\sqrt{7\left( {{\sinh }^{2} }t+1 \right)}

Now I could use the property of hyperbolic functions: {{\cosh }^{2} }x-{{\sinh }^{2} }x=1 :

\sqrt{{{x} ^{2} }+7}=\sqrt{7\left( {{\cosh }^{2} }t-1+1 \right)}

And I have neat:

\sqrt{{{x} ^{2} }+7}=\sqrt{7} \cosh t

Substituting all this into the integral, I would have:

\int{\frac{dx}{\sqrt{{{x}^{2}}+7}}}=\int{\frac{\sqrt{7}\cosh tdt}{\sqrt{7}\cosh t}}=\int{dt}=t+C

Now, since I the substitution:

\sqrt{7} \sinh t=x /:\sqrt{7}

\sinh t=\frac{x} {\sqrt{7} }

To determine t from it, I apply on both sides the inverse function of the hyperbolic sine and I have:

t=arsinh\frac{x} {\sqrt{7} }

or otherwise writing:

t={{\sinh }^{-1} }\frac{x} {\sqrt{7} }

Coming back to integral:

\int{\frac{dx}{\sqrt{{{x}^{2}}+7}}}=\int{\frac{\sqrt{7}\cosh tdt}{\sqrt{7}\cosh t}}=\int{dt}=t+C=arsinh \frac{x}{\sqrt{7}}+C

… general formula for an elementary integral: \int{\frac{dx} {\sqrt{{{x} ^{2} }+q}}}=\ln \left| x+\sqrt{{{x} ^{2} }+q} \right|+C can be expressed as:

\int{\frac{dx} {\sqrt{{{x} ^{2} }+q}}}=arsinh \frac{x} {\sqrt{q} }+C– for q>0

or:

\int{\frac{dx} {\sqrt{{{x} ^{2} }+q}}}=arcosh \frac{x} {\sqrt{q} }+C– for q<0

These formulas can be derived using the substitution \sinh t=x or \cosh t=x (depending on the sign of q). I already showed it above on a specific example for q=7 (q > 0).

Attention

During classes, professors often REQUIRE the use of the formula: \int{\frac{dx} {\sqrt{{{x} ^{2} }+q}}}=arsinh \frac{x} {\sqrt{q} }+C and they don’t even want to hear about the formula: \int{\frac{dx} {\sqrt{{{x} ^{2} }+q}}}=\ln \left| x+\sqrt{{{x} ^{2} }+q} \right|+C.

Or even better, they don’t allow you to use the formula at all, they just want you to solve such integrals by substituting hyperbolic functions.

So you have to watch out for that. It’s best to erase (that’s what they used to say my ancient times of pencils) the logarithm formula and replace it with the area sine formula.

Also remember that hyperbolic functions may “pop up” somewhere at the end of the task, for example in the integral:

\int{\frac{{{x} ^{2} }}{\sqrt{{{x} ^{2} }-x+1}}dx}

First, we need to move it using known methods, i.e. the method of indefinite coefficients, then disarm the integral by switching to the canonical form, etc. (I show how to solve such integrals in the Indefinite Integrals Course ) – only at the end will we have an integral to calculate in which it will “pop out” formula with area sine (or area cosine).

End

And that’s it, I hope it’s mysterious {{\sinh }^{-1} }x that sometimes appears in Wolfram’s results will no longer be so strange to you.