Asymptotes – Lecture 4
Topic: “Famous” Asymptotes of Functions
Summary
The topic of asymptotes at university level is not something completely new. Many graphs of functions known from high school already have asymptotes, and in some cases they can even be determined without calculating limits. In this lecture, we will review several popular functions that possess asymptotes.
Asymptotes of Trigonometric Functions
Let us take a look at the graph of the function ![]() :
:
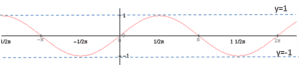
Do you think the lines y=1 and y=-1 are asymptotes of the graph?
The correct answer is: of course NOT. Why?
From an intuitive point of view, an asymptote is “something” that the graph of a function gets closer and closer to. In the sine graph, however, instead of approaching the lines y=1 or y=-1, the function periodically moves away from them and then gets closer again.
Now, being more precise, the line y=a is a horizontal asymptote of a function f(x) if the following limit exists:
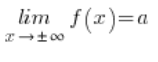
In our case, the limit of sin x as ![]() :
:
![]() – does not exist.
– does not exist.
Obviously, the same applies to cos x.
The function tan x, however, has vertical asymptotes:
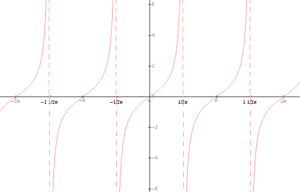
We can see that this function has infinitely many two-sided vertical asymptotes given by: ![]() , where k is any integer. Example equations of these asymptotes are:
, where k is any integer. Example equations of these asymptotes are: 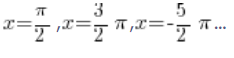
To find the vertical asymptotes of tan x, we set its argument equal to ![]() and solve the equation (which is equivalent to determining the domain of the tangent function).
and solve the equation (which is equivalent to determining the domain of the tangent function).
Example
Find the equations of the asymptotes of the function
We set the argument of the tangent equal to ![]() :
:
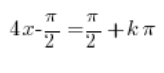
We move ![]() to the right-hand side:
to the right-hand side:
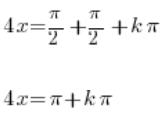
We divide both sides by 4:
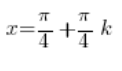
These are exactly the equations of the two-sided vertical asymptotes we were asked to find.
The function cot x also has vertical asymptotes:
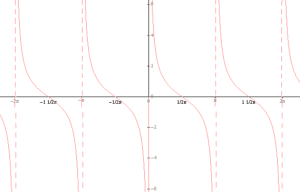
Their equations are the lines: ![]() .
.
Asymptotes of Inverse Trigonometric Functions
Inverse trigonometric functions are the inverse functions of the trigonometric ones. We denote them by: arcsin x, arccos x, arctan x, arccot x. Since sin x and cos x do not have asymptotes, it would be rather surprising if their inverse functions had any 🙂
The graph of arctan x, however, has horizontal asymptotes:
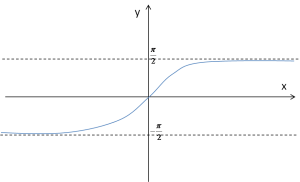
As ![]() the horizontal asymptote of arctan x is the line
the horizontal asymptote of arctan x is the line ![]() , and as
, and as ![]() it is the line
it is the line 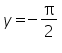 .
.
The graph of arccot x also has horizontal asymptotes:
As ![]() the equation of the horizontal asymptote is the line
the equation of the horizontal asymptote is the line ![]() , and as
, and as ![]() it is the line
it is the line ![]() .
.
Asymptotes of Exponential Functions
By an “exponential function” we mean a function of the form ![]() , where a>0 and a\ne 1.
, where a>0 and a\ne 1.
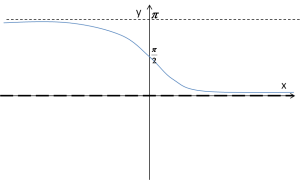
If a>1 , its graph looks approximately like this:
It has only one horizontal asymptote: the line ![]() as
as ![]() .
.
If a<1 , the graph takes the form:
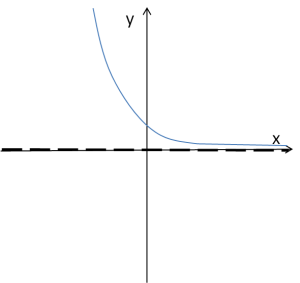
In this case, the line ![]() is the horizontal asymptote as
is the horizontal asymptote as ![]() .
.
Asymptotes of Logarithmic Functions
Logarithmic functions of the form ![]() for a>0 and a\ne 1 are inverse functions of exponential ones, so we expect vertical asymptotes. Indeed, regardless of which type of graph we draw (its shape depends on a)…
for a>0 and a\ne 1 are inverse functions of exponential ones, so we expect vertical asymptotes. Indeed, regardless of which type of graph we draw (its shape depends on a)…
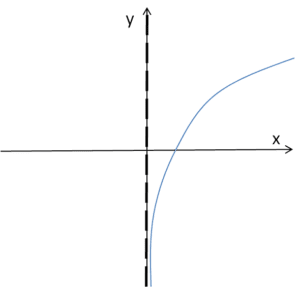
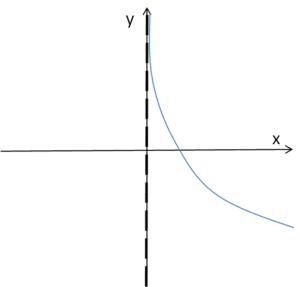
We can see that, regardless of a, the line ![]() is the equation of a vertical asymptote (but only one-sided!).
is the equation of a vertical asymptote (but only one-sided!).
Asymptotes of Homographic Functions
We encountered homographic functions in high school. They were special types of rational functions of the form:
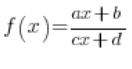 – where the constants a, b, c, d had to satisfy certain conditions, which we will skip for now 🙂
– where the constants a, b, c, d had to satisfy certain conditions, which we will skip for now 🙂
Using specific transformations, this function could be rewritten in the so-called “canonical form”:
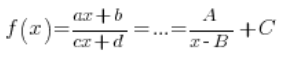
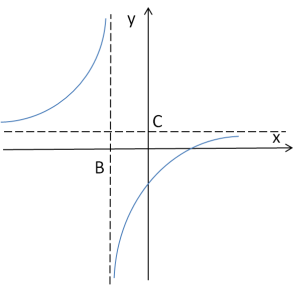
From this form, we can immediately read off the equation of the horizontal asymptote: ![]() and the vertical asymptote:
and the vertical asymptote: ![]() .
.
On the graph, it would look like this:
Click to review how to calculate oblique asymptotes in rational functions (previous Lecture) <–
Click to move on to the definition of extrema of functions (next Lecture) –>
Click to return to the page with lectures on analyzing functions
