Extrema of Functions – Lecture 8
Topic: Calculating Extrema of Functions Using Higher-Order Derivatives (A Sufficient Condition for the Existence of an Extremum Using Higher-Order Derivatives)
We already know how to calculate extrema of functions by observing changes in monotonicity in a neighborhood of a point, or by analyzing the sign of the first derivative in that neighborhood (which is essentially the same thing).
However, we can approach the problem differently and determine extrema by calculating higher-order derivatives (most often the second derivative is enough) and checking their signs.
Take a point 
, where the value of the first derivative equals zero, that is 
. Instead of drawing graphs, sign charts, and tables, we compute the second derivative (that is, the derivative of the derivative) 
. Then we calculate its value at the point by simply substituting it into the expression.
If the number we obtain is negative, the function attains a local maximum at that point. If the number is positive, the function attains a local minimum at that point. If the number equals zero, we are still stuck and may need to compute higher-order derivatives, as we will see after the example…
Example
Let us calculate the extrema of the function 
We compute its derivative and obtain: 
We set the derivative equal to zero and determine the points where it equals zero:
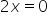
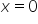
The point where the function might attain an extremum is 
. To verify whether an extremum is actually attained there, we compute the second derivative:
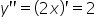
We calculate its value at the point , substituting 
for x. In this simple example, the second derivative does not even contain x, so we immediately check its sign. It is positive (
), therefore the function attains a local minimum at .
What if the second derivative at equals zero? Then we compute the third derivative and check its value at that point. If it also equals zero, we compute the fourth derivative, and so on, until we reach one that does not vanish at the point .
Then the following holds:
– if the first non-zero derivative is of odd order, the function does not attain an extremum at that point
– if the first non-zero derivative is of even order, then:
• if its value at is positive, the function attains a local minimum at that point
• if its value is negative, the function attains a local maximum at that point
Some professors require you to calculate extrema in this way — so good luck 🙂
While writing this post, I used:
1. “Differential and Integral Calculus. Vol. I.” G.M. Fichtenholz. 1966 edition.
Click to review another sufficient condition for the existence of an extremum (previous Lecture) <–
Click to return to the page with lectures on analyzing functions