Asymptotes Lecture 1
Topic: Asymptotes – definition
Summary
In this article we define limits of functions that diverge to infinity either in the argument or in the value. We will define them using sequences (thus applying Heine’s definition). We will also show their direct connection to vertical and horizontal asymptotes of a function’s graph.
We will need:
- Heine’s definition of an improper limit of a function
Limits of functions with infinity as the value and arguments approaching a number (vertical asymptotes of the graph)
Let us imagine the situation shown in the graph:
This is a fragment of the graph of the function 
. We see that for arguments x approaching 1 from the right, the corresponding function values become larger and larger – they diverge to infinity. Formally, we would write:
If for every sequence of arguments approaching from the right, the corresponding sequence of function values diverges to infinity (or minus infinity), we say that the function has a right-sided infinite limit at this point, which can be written as:
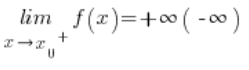
From the graph it is clear that the geometric interpretation of such a limit is simple: the graph has a right-sided vertical asymptote (a line to which the graph “approaches” from the right) with equation 
.
It is not difficult to imagine a left-sided vertical asymptote: this would correspond to a left-sided infinite limit, i.e. the sequences of arguments in the definition would approach 
from the left.
The definition of a general infinite limit of a function at a point (that is, a two-sided vertical asymptote on the graph) would be as follows:
If for every sequence of arguments approaching , the corresponding sequence of function values diverges to infinity (or minus infinity), we say that the function has an infinite limit at this point, which can be written as:
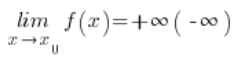
An interesting case occurs when, for example, the function approaches 
from the left and 
from the right.
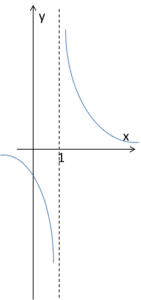
In that case, the limit of the function at the point does not exist (the left-hand and right-hand limits are different) – but a two-sided vertical asymptote still does (because both the left- and right-sided vertical asymptotes exist). On the graph, this could look like:
Limits of functions for arguments diverging to 
(or ) – horizontal asymptotes
Let us again consider the situation shown in the graph:
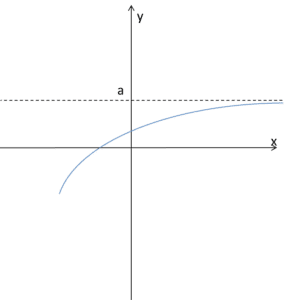
Notice that for arguments x diverging to infinity, the corresponding values converge to the number ‘a’. More precisely, we would write:
The function has limit a as x approaches (), if for every sequence of arguments diverging to () the corresponding sequence of values converges to a, which can be written as
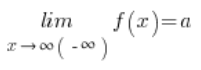
Such situations have their geometric interpretation on the graph as “horizontal asymptotes” of the function – that is, horizontal lines to which the graph “approaches” as x tends to plus or minus infinity.
Click here to see how to define oblique asymptotes (next Lecture) –>