Co to są asymptoty pionowe i poziome?

Asymptoty Wykład 1

Temat: Asymptoty – definicja

Streszczenie

W artykule zdefiniujemy granice funkcji rozbiegające do nieskończoności w argumentach, lub w wartościach. Będziemy definiować je przy pomocy ciągów (wykorzystując więc jakby definicję Heine’go). Przedstawimy także, jaki jest ich bezpośrednie przełożenie na asymptoty pionowe i poziome wykresu funkcji.

Potrzebne nam będą:

• definicja Heinego granicy niewłaściwej funkcji

Granice funkcji z nieskończonością w wyniku i argumentach dążących do liczby (asymptoty pionowe wykresu)

Wyobraźmy sobie sytuację jak na wykresie:

Jest to fragment wykresu funkcji . Widzimy, że przy argumentach x zbliżających się do 1 z prawej strony odpowiadające im wartości funkcji są coraz większe i większe – rozbiegają w nieskończoność. W sposób ścisły napisało by się, że:

Jeżeli dla każdego ciągu argumentów dążącego do z prawej strony odpowiadający im ciąg wartości rozbiega w nieskończoność (lub minus nieskończoność), mówimy, że funkcja w tym punkcie ma granicę nieskończoną prawostronną, co zapisać można jako:

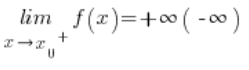
Z wykresu wynika wyraźnie, że interpretacja geometryczna istnienia takiej granicy jest prosta: wykres ma asymptotę pionową prawostronną (prostą, do której jakby “zbliża się” wykres z prawej strony) o równaniu .

Nietrudno wyobrazić sobie asymptotę pionową lewostronną: była by to granica nieskończona lewostronna, tzn. ciągi argumentów z definicji zbiegały by do z lewej strony.

Definicja ogólnej granicy nieskończonej z funkcji w punkcie (czyli asymptoty pionowej obustronnej na wykresie) wyglądała by tak:

Jeżeli dla każdego ciągu argumentów dążącego do z odpowiadający im ciąg wartości rozbiega w nieskończoność (lub minus nieskończoność), mówimy, że funkcja w tym punkcie ma granicę nieskończoną, co zapisać można jako:

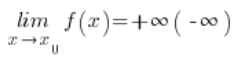
Ciekawym przypadkiem jest granica funkcji, która na przykład z lewej strony wychodzi , a z prawej .

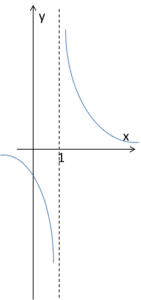
Wtedy granica funkcji w punkcie nie istnieje (granica lewostronna i prawostronna wyszły różne) – ale asymptota pionowa obustronna jak najbardziej (bo asymptoty pionowa lewo i prawostronna istnieją). Na wykresie wyglądać by to mogło tak:

Granice funkcji przy argumentach rozbiegających w (lub ) – asymptoty poziome

Weźmy znowu sytuację jak na wykresie:

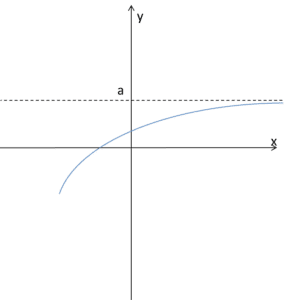Zauważmy, że przy argumentach x rozbiegających w nieskończoność odpowiadające im wartości zbiegają do liczby ‘a’. Ściślej napisało by się:

Funkcja osiąga granicę a przy x dążącym do (), jeżeli dla każdego ciągu argumentów rozbiegającego w () odpowiadający mu ciąg wartości zbiega do a, co można zapisać jako

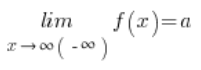
Tego typu sytuacje mają swoją interpretację geometryczną na wykresie jako “asymptoty poziome wykresu funkcji” – czyli proste poziome, do których “przybliża” się wykres funkcji przy x dążącym do plus lub minus nieskończoności.

Kliknij, aby zobaczyć, jak zdefiniować asymptoty ukośne (następny Wykład) –>

Kliknij, aby powrócić na stronę z wykładami o badaniu przebiegu zmienności funkcji