Limit of a Sequence

Limit of a Sequence – Lecture 1

Topic: Limit of a sequence – intuitive introduction and definition

Summary

In this article, I will explain what the limit of a sequence actually is. I will also explain in more detail how the definition of this limit should be understood.

What is a sequence?

Before we move on to what the limit of a sequence is, we must first explain what a sequence actually is. A numerical sequence is a list of numbers arranged in a specific order, for example:

1, 2, 4, 7, 10

Above we have a five-term sequence. The order is important. For example:

2, 1, 4, 7, 10

This is a completely different sequence.

When discussing the limit of a sequence, we will work with infinite sequences, for example:

-4, -1, 2, 5, 8, 11, …

Sequences can be represented by listing their first few terms or, if possible, by giving a formula for any term (for example, the hundredth term). Such a formula for the last sequence listed above (-4, -1, 2, 5, 8, 11, …) would look like this:

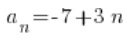
The variable n in the formula denotes the index of the term of the sequence. Let’s check if it works:

First term of the sequence: – correct (-4, -1, 2, 5, 8, 11, …)

Second term of the sequence: – correct (-4, -1, 2, 5, 8, 11, …)

etc.

Examples of sequences. Convergent sequences. Terms of a sequence on the number line.

To understand what the limit of a sequence is, it is very helpful to graphically mark the terms of the sequence on the number line (remember that from now on we are always talking about infinite sequences).

Let us take our sequence -4, -1, 2, 5, 8, 11, … (whose general term is given by the formula ). If we marked its first terms on the number line, it would look like this:

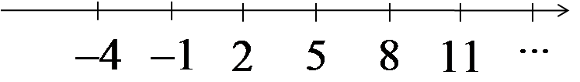
Notice that if we marked its subsequent terms (14, 17, …) on the number line, we would NOT be getting closer to any number on the line. On the contrary – we would be “running away” further and further towards infinity.

Now consider another sequence:

0, -2, -4, 0, 7, 1, -2, 2, 2, …

Finding a general formula for the n-th term of this sequence is rather impossible, because its terms arise quite chaotically and without any clear pattern (although some people believe there is ALWAYS a formula). If we marked these terms on the number line, we would get:

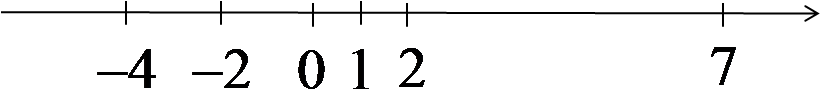
Marking subsequent terms, they would jump back and forth on the number line, NOT approaching any number. Such sequences also exist.

Now let us look at the following sequence:

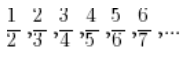
We can observe that the numerators are consecutive natural numbers, and the denominators are numbers greater by 1. The general term of this sequence would be . If we mark the terms of this sequence on the number line, we will notice one thing:

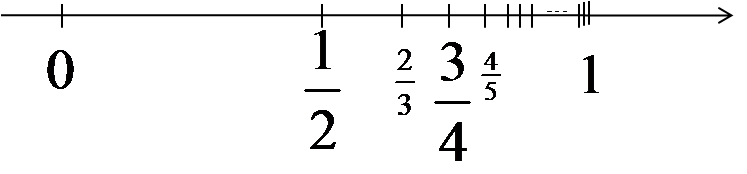
The successive terms of this sequence get closer and closer to the number 1. For example, the hundredth term (which we can compute by substituting n = 100 into the formula ) equals – very close to 1. The 101st term is even closer. The 102nd – even closer. The thousandth term is already “almost” 1.

As we take larger and larger term indices, we get closer and closer to 1. Although no term of the sequence is ever equal to 1 (because a number divided by a number greater by 1 is never equal to 1), we can say that this sequence HAS A LIMIT equal to 1.

What we have so far is an informal, intuitive understanding of the limit of a sequence. I have not precisely defined what “for larger and larger” and “closer and closer” mean. We will do that in the next part.

Before we define it rigorously, we must recall one important thing: how to compute the distance between two points on the number line.

Formula for the distance between two points on the number line

Consider the number line and two numbers on it (for variety, one positive and one negative):

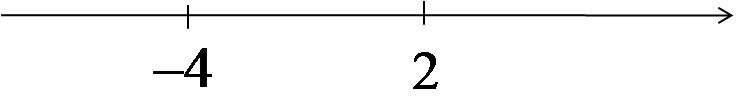
We all know that the distance is 6, but how do we compute it quickly?

One way is to subtract the smaller number from the larger one. In our case, subtract -4 from 2. The result is .

However, this requires comparing the numbers first. When dealing with variables, this can be inconvenient.

Another method is to subtract the numbers in any order and take the absolute value of the result. For example, subtract 2 from -4 to get , or subtract -4 from 2 to get .

Thus, the distance between two numbers on the number line is the absolute value of their difference.

Definition of the limit of a sequence

Let us now move back to the definition of the limit of a sequence.

Definition

A number g is called the limit of a sequence if:

\underset{\varepsilon >0}{\mathop{\forall }}\,\underset{N}{\mathop{\exists }}\,\underset{n>N}{\mathop{\forall }}\,\left| {{a}_{n}}-g \right|<\varepsilon

This definition means:

“For every ε greater than zero, there exists a number N such that for every n greater than N, the distance between aₙ and g is smaller than ε.”

No matter how small ε is, we can always find such an N. Therefore, the limit of the sequence is equal to 1.