Euler Substitution of the First Kind (for a>0) – Review
In the previous post:
Euler Substitution of the First Kind
we dealt with integrals of the type:
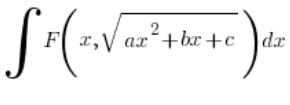 ,
,
where a>0.
We also solved an example integral that meets this condition, i.e.
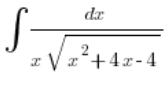
But what if ![]() in the trinomial is negative (the case when a=0 can be ignored because it would no longer be a quadratic trinomial, and the integral can be solved by a simpler substitution
in the trinomial is negative (the case when a=0 can be ignored because it would no longer be a quadratic trinomial, and the integral can be solved by a simpler substitution ![]() than the Euler substitution) ?
than the Euler substitution) ?
Then the second type of Euler substitution might help us (but it might not…):
Euler Substitution of the Second Kind (for c>0)
Having an integral of the type:
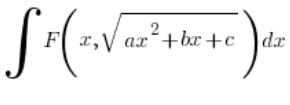 ,
,
where c>0, we use a substitution of the type:
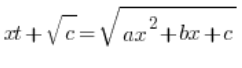 ,
,
which we again square on both sides, where this time the terms with ![]() cancel out, and then we divide both sides by
cancel out, and then we divide both sides by ![]() to get a linear dependency, from which we solve using the variable
to get a linear dependency, from which we solve using the variable ![]() in order:
in order:
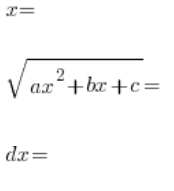
We substitute all this into the integral:
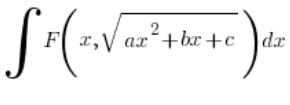
and we end up again with a rational integral, which – I repeat – is generally tedious.
Let’s proceed with an example.
Example
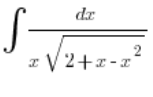
In the quadratic trinomial, the order of terms is slightly changed, but it’s clear that ![]() . That means
. That means ![]() is not greater than
is not greater than ![]() (so we won’t use the first kind of Euler substitution), but c>0 (so we’ll use the second kind).
(so we won’t use the first kind of Euler substitution), but c>0 (so we’ll use the second kind).
We substitute:
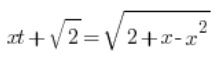
We square both sides:
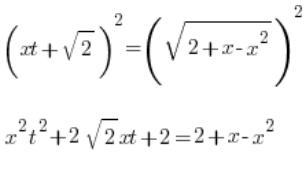
The 2 term cancels out (as it should):
![]()
And now something that wasn’t in the first kind of substitution, we divide both sides by x:
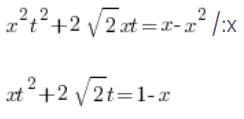
Next we solve for x:
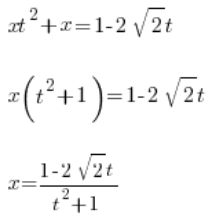
We have x solved in terms of the variable t. Now we solve for 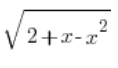 . Initially, we had the substitution:
. Initially, we had the substitution:
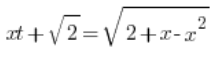
![]() is already solved, so we just plug it in:
is already solved, so we just plug it in:
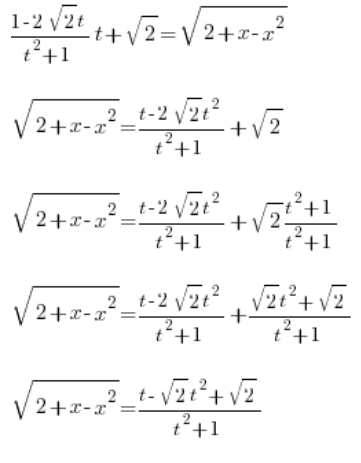
We only have to solve for ![]() . We calculate it by taking the derivative of
. We calculate it by taking the derivative of ![]() :
:
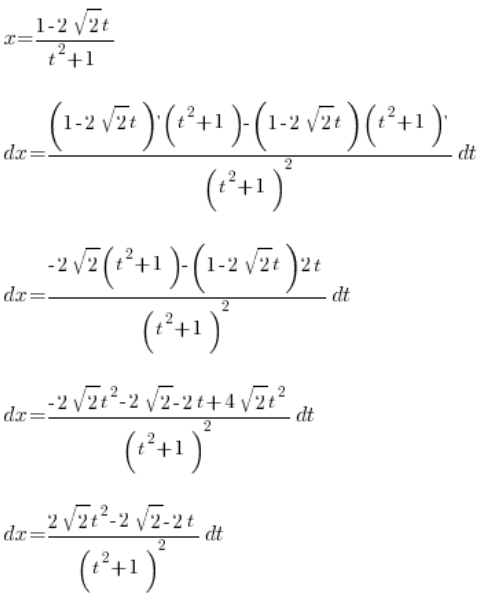
We have thus solved:
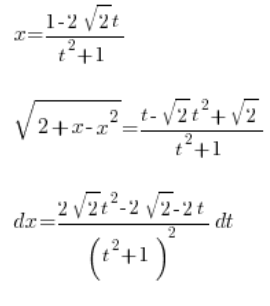
, all using the variable ![]() . We take the integral:
. We take the integral:
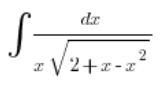
and substitute:
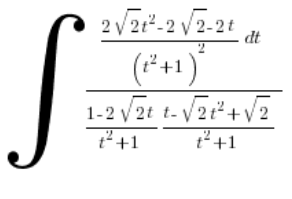
Let’s clean up:
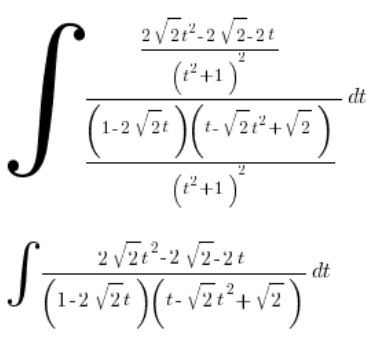
Returning to the substitution:
\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+CWe still need to return from t to x. Our Euler substitution was
xt+\sqrt{2}=\sqrt{2+x-{{x}^{2}}}From which
t=\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x}Thus our solution is
\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x} \right|+CWhat about other cases?
We know that when in the integral:
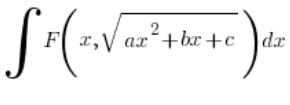
- a>0 – we use the first kind of substitution
- c>0 – we use the second kind of substitution
But what if neither ![]() nor
nor ![]() are greater than zero? We’ll discuss this in the next post, where I’ll cover the third kind of Euler substitution and show that the topic will be exhausted, i.e., for each type of integral:
are greater than zero? We’ll discuss this in the next post, where I’ll cover the third kind of Euler substitution and show that the topic will be exhausted, i.e., for each type of integral:
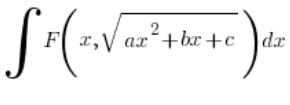
…we’ll choose one of the three kinds of substitution.


