This post is already the third in a row where I want to draw your attention to things that are worth reviewing at the very beginning of your mathematics studies at university. A quick review of them will make your life in university much easier. In previous posts, I discussed the topics of:
Geometric interpretation of absolute value
Today it’s the turn of the quadratic function.
Quadratic function? But we did that for two months…
The topic of the quadratic function is, of course, very broad, and I don’t mean at all that you should take a high school textbook and go through the entire chapter from cover to cover.
Let’s just focus on a few important details, nuances, and traps.
Quadratic function vs. quadratic equation
Quadratic function is, of course, something like this:
![]() or:
or: 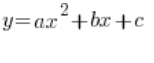
Where ![]() are any numbers. Examples of quadratic functions are:
are any numbers. Examples of quadratic functions are:
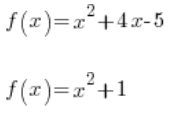
and so on…
The concept of a quadratic function should be distinguished from the concept of a quadratic equation, for example:
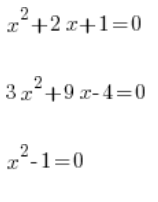
and so on…
It’s not the same!!!!
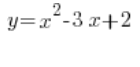 is a quadratic function, while
is a quadratic function, while 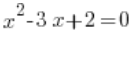 is a quadratic equation.
is a quadratic equation.
Not distinguishing between a function and an equation often leads to…
Gruesome mistake number 1
When calculating derivatives, for example, and given a function:
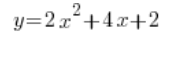
People often do something like this:
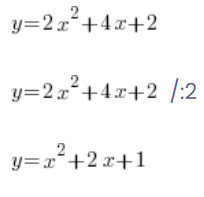
…and continue calculating whatever is needed.
They make this mistake because they remember they could do something like this with equations:
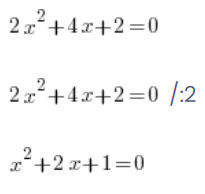
…and with equations, everything is okay, you can divide both sides, 0 on the right divided by 2 indeed gives 0, and the equations are equivalent (have the same solutions).
But you can’t do this with functions – you’d have to somehow divide that y on the left as well, etc. By simply dividing the value of the function by 2, you’ll get a different function!
What should you review from functions?
Not much. Actually, only two forms of the function: canonical and factored.
The canonical form of a quadratic function
I assume we already have the general form of a quadratic function:
![]()
Its canonical form is:
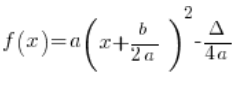
That is:
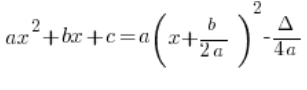
What a, b, and ![]() are is well-known, few people have a problem with
are is well-known, few people have a problem with ![]() .
.
You can even notice that if we factor out ![]() in the canonical form, we’ll get:
in the canonical form, we’ll get:
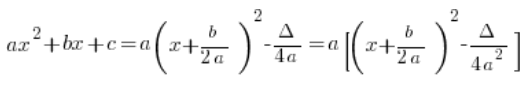
…which can sometimes be useful and sometimes not necessarily.
If you learned this by calculating the coordinates of the vertex (usually as ![]() and
and ![]() ) and plugging into the formula:
) and plugging into the formula:
![]() then it’s, of course, a bit roundabout, but also cool.
then it’s, of course, a bit roundabout, but also cool.
Remember ![]() at the beginning of the canonical form!
at the beginning of the canonical form!
The factored form of a quadratic function (its factorization):
Returning now to our general quadratic function:
![]()
We will often need to “factor it,” using the factored form of a quadratic function:
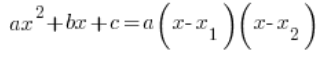
Where ![]() and
and ![]() are calculated from the well-known and loved formulas:
are calculated from the well-known and loved formulas:
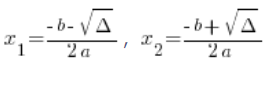
Here too, you must remember ![]() at the beginning of the formula!!!
at the beginning of the formula!!!
Also note that these ![]() and
and ![]() do not always exist (if Δ is negative, they do not exist), which means the function cannot always be written in factored form, that is, a quadratic function cannot always be factored.
do not always exist (if Δ is negative, they do not exist), which means the function cannot always be written in factored form, that is, a quadratic function cannot always be factored.
What should you review from quadratic equations?
With quadratic equations, I suppose things aren’t too bad. We usually manage to solve the general equation:
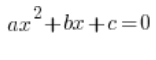
For example:
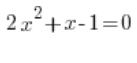
We simply calculate:
![]()
Then, if Δ is non-negative, solve the equation:
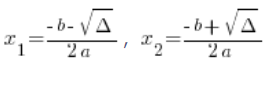
Remember, there’s ![]() in the denominator, not just 2!
in the denominator, not just 2!
However, I’d like to stop at a particular case of the equation:
![]()
Here, many mistakes occur. For example:
Gruesome mistake number 2
![]()
![]()
What’s the mistake exactly? The number 2 is indeed a solution to the equation ![]() , but the second solution to this equation, namely the number -2, has been completely omitted. It should be:
, but the second solution to this equation, namely the number -2, has been completely omitted. It should be:
![]()
![]()
Negative solutions can only be ignored in geometry (because distance cannot be negative).
Another problem with the equation in the form: ![]() is:
is:
Gruesome mistake number 3
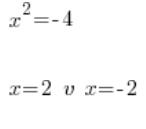
Which is, of course, nonsense because 2 squared does not give -4. In fact, nothing squared gives -4 (those who have already studied complex numbers, keep quiet). The equation:
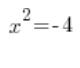
…has no solutions.
So, you need to be vigilant. The equation ![]() has two solutions, and the equation
has two solutions, and the equation ![]() has no solutions at all.
has no solutions at all.
I invite you to calmly review everything that has been said so far and, of course, to ask questions in the comments.


