Canonical Form of a Quadratic Function in Rational Integrals
Krystian Karczyński
Founder and General Manager of eTrapez.
Graduate of Mathematics at Poznan University of Technology. Mathematics tutor with many years of experience. Creator of the first eTrapez Courses, which have gained immense popularity among students nationwide.
He lives in Szczecin, Poland. He enjoys walks in the woods, beaches and kayaking.
I get a lot of questions about the formula for the canonical form of a quadratic function introduced in my Course on Indefinite Integrals.
The formula:
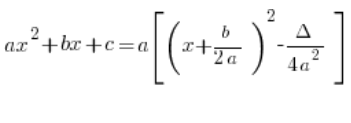
appears in the scheme for solving rational integrals in Lesson 5 of the course:
Why is there a^2?
The problem is that at first glance, it looks different from the canonical form known from high school:
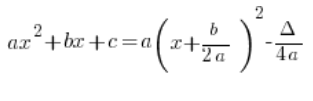
The standard question here is: “Why do you have 
in the denominator?”
Transforming the formula
It’s enough to notice that if in the formula:
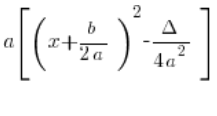
we multiply 
by the square bracket, we get exactly the formula:
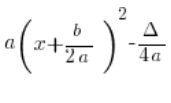
(after multiplying by the term 
it cancels out and we get 
)
Therefore, both forms are equivalent, which means simply:
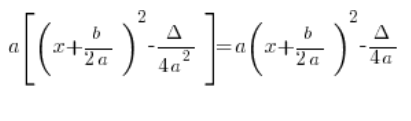
So why introduce this formula with the square bracket and a outside the bracket? Because in rational integrals, it is more convenient 🙂
In the later stages of calculating the integral, you will still need to extract in front of the integral sign (and first in front of the bracket in the denominator), so why wait? 🙂
Are you looking for college or high school math tutoring? Or maybe you need a course that will prepare you for the final exam?
We are "eTrapez" team. We teach mathematics in a clear, simple and very precise way - we will reach even the most knowledge-resistant students.
We have created video courses translated in an easy, understandable language, which can be downloaded to your computer, tablet or phone. You turn on the video, watch and listen, just like during private lessons. At any time of the day or night.
