Ekstrema Funkcji Wykład 5
Temat: Ekstrema funkcji.
Streszczenie
Na wykładzie wprowadzę intuicyjnie pojęcie ekstremów funkcji, zdefiniuję też je w sposób ścisły.
Co to jest ekstremum funkcji?
Słowo extremum pochodzi z łaciny i oznacza skrajne. Są dwa rodzaje ekstremów funkcji: minimum i maksimum. Z intuicyjnym rozumieniem tego pojęcia nie ma na ogół problemów:
Powyżej mamy wykres funkcji 
, który osiąga maksimum w punkcie 
.
Z minimum też, nie mamy żadnych problemów, prawda?
Powyżej mamy minimum funkcji w punkcie .
Jak się zastanowić, to nie ma w sumie problemu, żeby funkcja miała kilka ekstremów w różnych punktach:
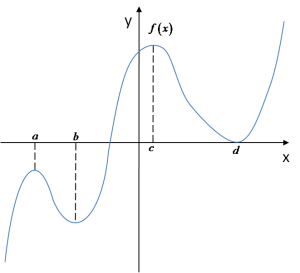
Powyższa funkcja ma minima w punktach: b i d; a maksima w punktach: a i c. Na podstawie powyższego wykresu zwrócić uwagę można na ważną rzecz: Uwaga (ważna rzecz) Minimów i maksimów funkcji nie można mylić z najmniejszymi/największymi wartościami funkcji. To coś zupełnie innego. No bo rzeczywiście – wartość funkcji w punkcie d (minimum) jest większa od wartości funkcji w punkcie a (maksimum). Niezbyt ściśle więc – ale obrazowo – “minimum” jest tu większe od “maksimum” (co do wartości funkcji). Przyjrzyj się wykresowi więc – jak opisał byś, czym jest ekstremum? Aby wprowadzić ścisłą i formalną definicję ekstremum przypomnimy sobie z poprzednich Wykładów, co to jest otoczenie punktu:
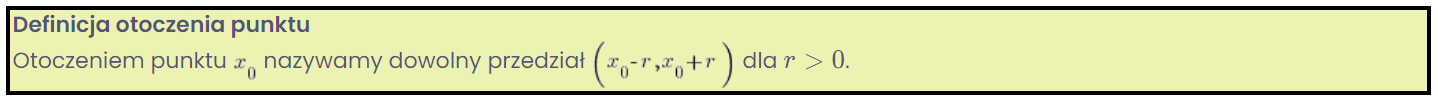
Na naszym wykresie zaznaczyłem dwa różne możliwe otoczenia punktu b (wybrałem sobie dwa różne 
). Oczywiście jest ich nieskończenie wiele:
Teraz, wiedząc już, czym jest otoczenie, zdefiniować możemy ekstrema funkcji.
Przyjrzyjmy się wykresowi naszej funkcji i zobaczmy, jak “działa” na nim ta definicja. Zaznaczamy jakieś byle jakie otoczenie punktu b: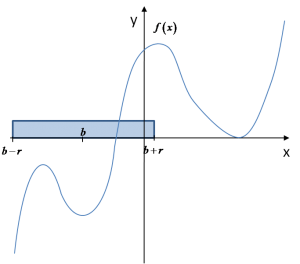 
Jakie wartości przyjmuje funkcja w punktach tego otoczenia? A jaką w punkcie b? Zobaczmy: 
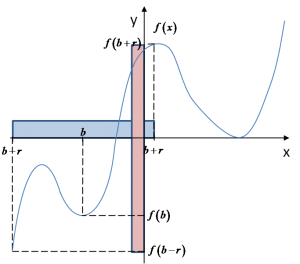Widać, że dla wartości funkcji w tym konkretnie wybranym otoczeniu punktu b NIE jest spełniony warunek z definicji, tzn:
– czyli wartość funkcji w punkcie
– czyli wartość funkcji w punkcie Warunek bowiem mówi nam, że wartości funkcji w tym punkcie, gdzie ma być niby ekstremum (u nas jest to punkt b) powinna być mniejsza, od wartości w DOWOLNYM pozostałym punkcie tego przedziału. Tymczasem na wykresie widać, że wartości funkcji 
nie jest najmniejsza dla x-sów z tego otoczenia. Tym bardziej nie ma co mówić o maksimum w punkcie b w tym otoczeniu. Czy oznacza to, że funkcja nie osiąga ekstremum w punkcie b? Nie! Przyjrzyjmy się uważnie definicji. Mamy w niej:
Funkcja
z tego otoczenia:…itd.Istotne w definicji jest słówko “istnieje”. Znaczy to, że wystarczy znaleźć byle jakie otoczenie punktu b, które spełnia warunek z definicji i wystarczy to, aby w punkcie b zostało osiągnięte ekstremum funkcji. No a z tym nie będzie już problemów, weźmy na przykład otoczenie: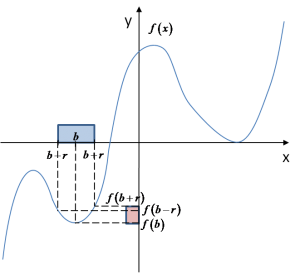 
Widać, że dla takiego otoczenia punktu b wartość funkcji w punkcie b rzeczywiście jest mniejsza od dowolnej innej wartości funkcji w punktach tego otoczenia, zatem warunek z definicji jest spełniony, czyli można powiedzieć, że funkcja osiąga minimum w punkcie b. Istnieje takie otoczenie, które spełnia warunek z definicji. Bardzo wytwornie i staroświecko można by powiedzieć: “istnieje takie otoczenie, które czyni zadość definicji” – wypróbujcie te słownictwo na profesorach, może będą tak zachwyceni, że zaliczą Wam semestr bez zaliczenia 🙂 Zwróćmy uwagę, że jeśli zdefiniujemy ekstrema funkcji w ten sposób (przez otoczenie punktu) funkcja będzie mogła osiągnąć ekstremum w punkcie tylko wtedy, kiedy będzie określona z obu stron . Na przykład: 
Ta funkcja nie osiąga ekstremum w punkcie 
(mimo, że osiąga w nim najmniejszą wartość). Nie ma takiego otoczenia, które spełniało by warunek z definicji, bo jakiekolwiek byśmy nie wzięli, na lewo od funkcja nie osiąga żadnych wartości, które można by porównać z wartością w punkcie . Nie dobierzemy otoczenia punktu , które zawierało by się w dziedzinie funkcji. Uwaga Aby odróżnić ekstrema funkcji od ich największy/najmniejszych wartości często stosuje się następujące słownictwo (dosyć dobrze związane z intuicją): ekstrema funkcji nazywa się ekstremami lokalnymi, a najmniejsze/największe wartości ekstremami globalnymi. Oczywiście kwestia nazewnictwa jest sprawą umowną. Co kto lubi. Powodzenia z ekstremami w uczelnianych bojach! 🙂
KONIEC
Pisząc tego posta korzystałem z…
1. “Rachunek różniczkowy i całkowy. Tom I.” G.M. Fichtenholz. Wyd. 1966.
Kliknij tutaj, aby przypomnieć sobie kilka asymptot znanych funkcji (poprzedni Wykład) <–
Kliknij tutaj, aby zobaczyć, jak ekstrema funkcji wiążą się z ich pochodnymi (następny Wykład) –>
Kliknij, aby powrócić na stronę z wykładami o badaniu przebiegu zmienności funkcji
Dalej kurde nie wiem co to ekstremum lokalne :< O co tu chodzi?? Coś tam się niby dowiedziałem
Panie Krystianie, jak to liczyć matematycznie bez patrzenia na wykres tylko z samego wzoru funkcji?
Matematycznie to mam pomysł, żeby przyrównać pochodną do 0 – wtedy dostaniemy przedziały mówiące gdzie funkcja maleje a gdzie rośnie – na podstawie tego wyznaczamy ekstrema?
Okej, udało mi się znaleźć, wikipedia ładnie to wyjaśnia:
Warunek konieczny i wystarczający istnienia ekstremum lokalnego
Funkcja ciągła fcolon [a,b]to mathbb{R}, różniczkowalna w przedziale (a,b), i mająca skończoną liczbę punktów stacjonarnych (tj. takich, w których zeruje się jej pierwsza pochodna)[5] ma w punkcie x_0in (a,b),:
minimum lokalne wtedy i tylko wtedy, gdy istnieje takie delta >0,, że:
f^prime(x_0)=0
f^prime(x) 0 dla x\in (x_0,x_0+delta)
maksimum lokalne wtedy i tylko wtedy, gdy istnieje takie delta >0,, że
f^prime(x_0)=0
f^prime(x)> 0 dla x\in (x_0-delta, x_0)
f^prime(x)< 0 dla x\in (x_0, x_0+delta)
Czy przy liczeniu ekstremów globalnych nie trzeba wyznaczać dziedzin funkcji?
a ja polecam 😉
Slaby wyklad, zdecydowanie nie polecam.
Witam, poszukuję programu, który wyliczyłby ekstrema globalne w danym obszarze/zbiorze, czy moge liczyć na pomoc? 🙂