W jednym z moich poprzednich artykułów przedstawiłam kilka przykładów modeli nieliniowych oraz sposoby, jak je sprowadzić do liniowych. Czyli dokonać tzw. linearyzacji.
To taka troszkę przeróbka, transformacja za pomocą pewnych metod matematycznych (np działania logarytmowania). Transformacja kojarzy mi się zawsze z „Transformerami” – w sumie oni też przekształcali się w samochody czy inne przedmioty. Może i ścisłej matematyki do tego nie wykorzystali, ale jednak jakaś tam „zamiana” była 🙂
Wspomniałam też o tym, że modele liniowe dzieliły się na liniowe względem parametrów oraz liniowe względem zmiennych. Czy to duża różnica? Otóż tak. Na dodatek ten pierwszy podział jest ważniejszy niż ten drugi. Bo zadaniem ekonometrii jest przede wszystkim estymacja parametrów, a jeżeli są one nieliniowe, to sprawy się komplikują…
Przykład 1
Popatrz na te dwa modele:
model nr 1: 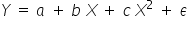 ,
,
model nr 2: 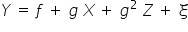 ,
,
gdzie X, Y, Z są zmiennymi, zaś a, b, c, f, g oznaczają parametry strukturalne oraz 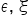 – składniki losowe.
– składniki losowe.
Ogólnie, w modelu typowo liniowym główną rolę odgrywa suma iloczynów typu 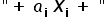 . To znaczy, że zarówno parametry, jak i zmienne powinny być jednocześnie w pierwszych potęgach, oraz zmienna objaśniana Y powinna być kombinacją liniową zmiennych objaśniających i różnych parametrów.
. To znaczy, że zarówno parametry, jak i zmienne powinny być jednocześnie w pierwszych potęgach, oraz zmienna objaśniana Y powinna być kombinacją liniową zmiennych objaśniających i różnych parametrów.
Tutaj tak nie jest. Dlatego też można śmiało stwierdzić, że w powyższym przykładzie oba modele są NIELINIOWE.
Jednakże, gdyby przypatrzeć się osobno zmiennym, a osobno na parametrom (w jakich są potęgach), to można powiedzieć, że model nr 1 jest liniowym modelem względem parametrów, natomiast model nr 2 jest liniowym modelem względem zmiennych.
Zobacz – niby nieliniowe, a jednak liniowe, przynajmniej częściowo 🙂
Pochodne cząstkowe względem parametrów
Skoro na początku wspomniałam, że kluczową rolę w ekonometrii odgrywa jednak liniowość modeli względem parametrów, to zapewne istnieje sposób, by ją jakoś konkretnie wskazać. I tak jest.
Wykorzystuje się do tego tzw. POCHODNE CZĄSTKOWE (nie, nie „czosnkowe”, bo zdarzało mi się nie raz i tak mówić) funkcji Y względem parametrów. Uwaga – NIE względem zmiennych objaśniających.
Dokładniej o pochodnych cząstkowych dowiedzieć się możesz z Kursu Pana Krystiana. Oczywiście zanim do nich przejdziesz, musisz mieć super opanowane zwykłe pochodne. Te również są omówione, ale w innym Kursie.
Do rzeczy.
Liczymy pochodne cząstkowe po parametrach. Czyli nie dla zmiennych X, Z, ale względem tych małych literek: a, b, c, f, g. Jeżeli każda z tych pochodnych jest NIEZALEŻNA od wszystkich parametrów modelu (czyli wynik pochodnej nie będzie zawierał tej małej literki), to taki model jest liniowy względem parametrów.
Policzmy pochodne cząstkowe modeli nr 1 oraz nr 2, czyli 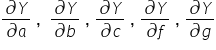 .
.
W pochodnych cząstkowych traktuję teraz daną literkę, np. „a” jako zmienną (wyobraź sobie że to jest „x„) a WSZYSTKIE pozostałe literki są nieważne, czyli traktujesz je wtedy jako STAŁĄ.
Tutaj przydadzą się dwa podstawowe wzory na pochodne związane ze stałą:
 (znasz na pewno bardziej wersję:
(znasz na pewno bardziej wersję:  )
)
oraz
 (w wersji wzorowej:
(w wersji wzorowej:  )
)
oraz oczywiście wszystkie inne wzory na pochodne, np 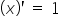 czy też
czy też 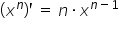 (akurat te mi się tu przydadzą).
(akurat te mi się tu przydadzą).
Tak więc w modelu nr 1: 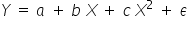
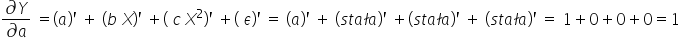
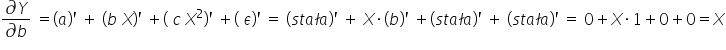
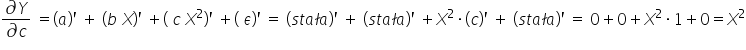
Czyli pochodne nie zależą od parametrów, więc model nr 1 jest liniowy względem parametrów.
Natomiast w modelu nr 2: 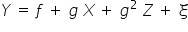
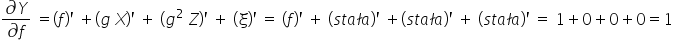
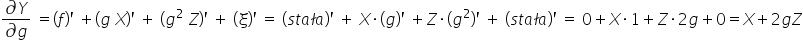
Tutaj już druga pochodna 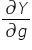 zależy od samego parametru g, dlatego też model nr 2 NIE jest liniowy względem parametrów.
zależy od samego parametru g, dlatego też model nr 2 NIE jest liniowy względem parametrów.
Pochodne cząstkowe względem zmiennych
Skoro już doszliśmy do pochodnych cząstkowych.
Oprócz liczenia ich względem parametrów, liczy się je oczywiście również względem zmiennych objaśniających 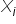 .
.
Jest to inna metoda przydatna przy określaniu związku funkcyjnego w modelach ekonometrycznych.
Najpierw wspomnę OGÓLNĄ INTERPRETACJĘ pochodnej cząstkowej jakiejkolwiek funkcji po jej zmiennej składowej, czyli 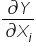 (często nazywaną funkcją krańcową):
(często nazywaną funkcją krańcową):
Jeżeli ….to co na dole… wzrośnie (ZAWSZE wzrośnie!) o
jednostkę, …pozostałe zmienne… pozostaną bez zmian (ceteris paribus), to …to co na górze.. zmienia się (wzrasta / maleje) o około ..wynik.. jednostek.
Dlatego też analiza wrażliwości zmiennej objaśnianej Y na przyrost (krańcowo mały, jednostkowy) wartości zmiennej objaśniającej 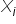 nam się tutaj przyda.
nam się tutaj przyda.
Jak to się ma do rozpoznawania rodzaju modelu?
Otóż w typowych modelach liniowych typu 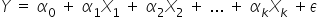 taka zmiana zmiennej Y powinna być STAŁA i równać się wartości parametru stojącego przy tej zmiennej, czyli
taka zmiana zmiennej Y powinna być STAŁA i równać się wartości parametru stojącego przy tej zmiennej, czyli 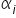 (oczywiście przy niezmienionych wartościach innych zmiennych – ceteris paribus). Przyrost ten nie zależy od zmiennej
(oczywiście przy niezmienionych wartościach innych zmiennych – ceteris paribus). Przyrost ten nie zależy od zmiennej 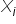 . Dlatego też składnik dotyczący tej zmiennej w modelu powinien mieć postać
. Dlatego też składnik dotyczący tej zmiennej w modelu powinien mieć postać 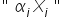 , czyli zbudować model liniowy.
, czyli zbudować model liniowy.
Wzięło się to stąd, że: 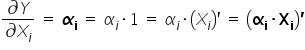 .
.
Stąd, jeśli policzysz pochodne cząstkowe po zmiennych objaśniających modelu 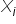 i w wyniku pojawią Ci się zmienne, lub nie same stałe parametry, to taki model jest nieliniowy.
i w wyniku pojawią Ci się zmienne, lub nie same stałe parametry, to taki model jest nieliniowy.
Wracając do Przykładu 1, popatrz, dlaczego są to modele wprost nieliniowe.
W modelu nr 1: 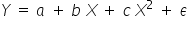
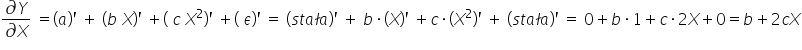
Ewidentnie nie jest to ani samo „b„ ani samo „c„.
Natomiast w modelu nr 2: 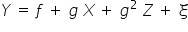
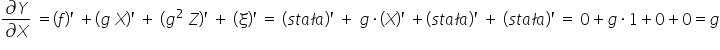
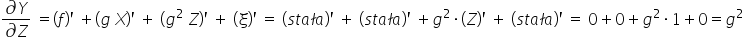
Obie pochodne wyszły równe stałej (liczbie). Jednak parametr dla drugiej pochodnej jest podniesiony do kwadratu, a to nam nie pasuje.
Elastyczność
Często w firmach czy wielkich przedsiębiorstwach analityków nie interesuje przyrost ilościowy, ale PROCENTOWY. To znaczy, że nie chcemy znać wiedzieć o ile jednostek (kilogramów, sztuk, mln zł, itp.) wzrośnie/spadnie zmienna objaśniana Y, ale o ile procent zmieni jej wartość, gdy wartość danej zmiennej 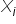 krańcowo wzrośnie.
krańcowo wzrośnie.
Przykład 2
Przedstawiono raport opisujący zależność sprzedaży czasopisma „Moje żubry” (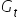 – w tys. sztuk), w zależności od wydatków na reklamę tej gazety (
– w tys. sztuk), w zależności od wydatków na reklamę tej gazety (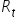 – w tys. zł). Otrzymano liniowy model ekonometryczny (już po oszacowaniu):
– w tys. zł). Otrzymano liniowy model ekonometryczny (już po oszacowaniu):
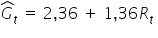
Jak już wspominałam wyżej, a także w moim wcześniejszym artykule, interpretacja oceny parametru w modelu typowo liniowym jest taka:
Wzrost (zawsze wzrost!) zmiennej objaśniającej 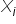 o 1 jednostkę pociąga za sobą zmianę (wzrost lub spadek – w zależności od znaku przy parametrze: „+” czy „–” ) zmiennej objaśnianej Y o wartość oszacowanego parametru
o 1 jednostkę pociąga za sobą zmianę (wzrost lub spadek – w zależności od znaku przy parametrze: „+” czy „–” ) zmiennej objaśnianej Y o wartość oszacowanego parametru 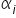 , oczywiście przy niezmienionych wartościach pozostałych zmiennych (ceteris paribus) – można by napisać jakich.
, oczywiście przy niezmienionych wartościach pozostałych zmiennych (ceteris paribus) – można by napisać jakich.
W tym przykładzie mielibyśmy:
Jeśli wartość wydatków na reklamę wzrośnie o 1 tysiąc złotych, to ilość sprzedanych egzemplarzy czasopisma „Moje żubry” wzrośnie o około 1,36 tys. sztuk (o około 1360 sztuk).
Teraz pytanie, czy 1360 sztuk sprzedanych gazet to dużo, czy mało? Zwłaszcza względem wzrostu wydatków na reklamę aż o tysiąc złotych?
Czy gdyby powiedzieć, że sprzedaż wzrosła o powiedzmy 10-15% to nie byłaby to bardziej jasna, dokładniejsza, trafiająca do odbiorcy liczba? Zwłaszcza że wiemy ile sprzedajemy, więc ten wzrost procentowy na sztuki łatwo byśmy policzyli.
Dlatego też innym ważnym pojęciem używanym w ekonometrii (jak i innych ekonomicznych dziedzinach) jest ELASTYCZNOŚĆ. Do niej też wykorzystuje się pochodne cząstkowe, tylko z lekką modyfikacją. Oto wzór:
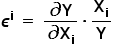 inaczej mówiąc:
inaczej mówiąc: 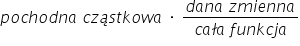 .
.
Do obliczeń można również wykorzystać pochodne logarytmiczne (do tego jednak musiałbyś przypomnieć rożne własności i działania na logarytmach), tzn.
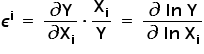
Wzór wzorem, interpretacja elastyczności idzie tak:
Jeżeli wartość zmiennej objaśniającej
wzrośnie o
(w procentach, a nie jednostkach!), to wartość zmiennej objaśnianej Y zmieni się (wzrost lub spadek – w zależności od znaku przy parametrze: „+” czy „–” ) o … wynik elastyczności… procent, przy niezmienionych wartościach pozostałych zmiennych (ceteris paribus).
Nie jest to trudne 🙂 Dla liniowych modeli ekonometrycznych interpretacja wyniku elastyczności jest identyczna jak dla oszacowanego parametru 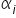 , tylko tyle, że w procentach, a nie zwykłych jednostkach.
, tylko tyle, że w procentach, a nie zwykłych jednostkach.
Na przykład, wartość 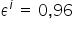 oznacza, że wraz ze wzrostem wartości zmiennej
oznacza, że wraz ze wzrostem wartości zmiennej 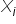 o
o 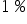 , wartość zmiennej Y wzrośnie o około
, wartość zmiennej Y wzrośnie o około 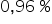 (a nie
(a nie 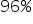 ) przy założeniu, iż wartości pozostałych zmiennych objaśniających nie ulegają zmianie.
) przy założeniu, iż wartości pozostałych zmiennych objaśniających nie ulegają zmianie.
Mam nadzieję, że po lekturze tego artykułu istota pochodnych cząstkowych i samej elastyczności nie będzie już taką tajemnicą i czymś obcym.
Podobnie rozpoznawanie modeli liniowych, tak ważnych w ekonometrii. Jak sam widzisz, wystarczy się nauczyć pewnego schematu, który powiela się w wielu innych aspektach, oczywiście z lekkimi modyfikacjami.
KONIEC

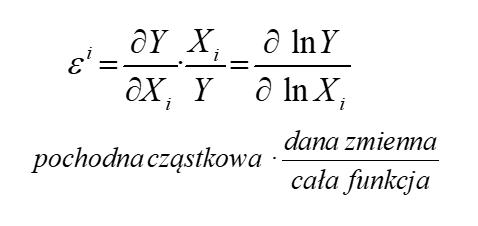
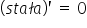 (znasz na pewno bardziej wersję:
(znasz na pewno bardziej wersję: 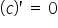 )
)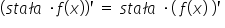 (w wersji wzorowej:
(w wersji wzorowej: 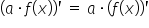 )
)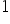 jednostkę, …pozostałe zmienne… pozostaną bez zmian (ceteris paribus), to …to co na górze.. zmienia się (wzrasta / maleje) o około ..wynik.. jednostek.
jednostkę, …pozostałe zmienne… pozostaną bez zmian (ceteris paribus), to …to co na górze.. zmienia się (wzrasta / maleje) o około ..wynik.. jednostek.