Was zum Quadrat ergibt 17? Nämlich unbestimmte Integrale und die Formel mit Arcustangens

Die Arctan-Formel in typischen unbestimmten Integralen

Wir haben uns daran gewöhnt, diese Formel zu verwenden: in „reinen“ Integral-Situationen,

wie zum Beispiel:

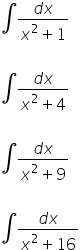
Dann verwandeln wir einfach…

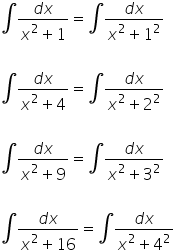
…und kommen elegant zum Ergebnis:

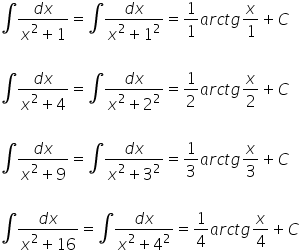
Die Arctan-Formel in untypischen Situationen bei unbestimmten Integralen

Und was machen wir mit diesem unbestimmten Integral:

? Was hoch zwei ergibt 17? Nichts? Nein… hoch zwei ergibt 17, also:

Generell gilt also, dass die Formel jedes unbestimmte Integral dieser Art handhaben kann, die Konstanten im Nenner müssen nicht so leicht als Quadrat darstellbar sein…

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.

Related Posts

Nachweis, dass sin(x) keinen Grenzwert erreicht, wenn x gegen Unendlich geht

Posted on

Die „Pi-mal-Daumen“ Schätzung des Ranges einer Matrix

Posted on

Probleme mit unbestimmten Symbolen (VIDEO)

Posted on

Leave a Reply

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert

Ihr Kommentar wird zusammen mit der obigen Signatur öffentlich auf unserer Seite verfügbar sein. Sie können Ihren Kommentar jederzeit ändern oder löschen. Der Verantwortliche für die persönlichen Daten, die in diesem Formular angegeben sind, ist eTrapez Usługi Edukacyjne E-Learning Krystian Karczyński. Die Regeln für die Datenverarbeitung und Ihre damit verbundenen Rechte sind in der Datenschutzrichtlinie beschrieben.