Trigonometrische Funktionen (verwendet in der trigonometrischen Form einer komplexen Zahl) sind ![]() -periodisch, was bedeutet, dass bei beliebigen Argumenten, die sich um z.B.
-periodisch, was bedeutet, dass bei beliebigen Argumenten, die sich um z.B. ![]() unterscheiden, dieselbe Wert annehmen.
unterscheiden, dieselbe Wert annehmen.
Zum Beispiel:
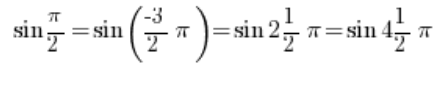
So nimmt beispielsweise eine komplexe Zahl in ihrer trigonometrischen Form:
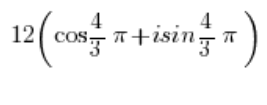
Dies ist dieselbe komplexe Zahl wie:
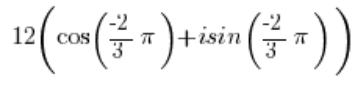
weil die Argumente der trigonometrischen Funktionen sich um ![]() unterscheiden.
unterscheiden.
Welche Argumente sollten in der trigonometrischen Form einer komplexen Zahl verwendet werden?
Welche Argumente werden üblicherweise verwendet? In Polen (und in meinem Kurs über komplexe Zahlen) aus dem Intervall ![]() . In älteren Lehrbüchern oder ausländischen Werken kann es jedoch das Intervall
. In älteren Lehrbüchern oder ausländischen Werken kann es jedoch das Intervall ![]() sein. Es ist wichtig, dies zu beachten, wenn man seine Berechnungen mit den Antworten aus dem Lehrbuch vergleicht.
sein. Es ist wichtig, dies zu beachten, wenn man seine Berechnungen mit den Antworten aus dem Lehrbuch vergleicht.


