Układy równań liniowych jednorodne to taki układy, w których wszystkie wyrazy wolne równe są 0.
Pokażę, jak rozwiązywać takie układy równań za pomocą rzędu macierzy.
Załóżmy, że zdefiniowaliśmy rząd macierzy jako: „liczba liniowo niezależnych wierszy i kolumn w macierzy”. Jakie już „na starcie” właściwości rzędów wynikają z tej definicji?
Po pierwsze, oczywiste jest, że rząd macierzy może być równy: 1, albo 4, albo czasami 0. Ale na pewno nie wyjdzie równy: -4, czy 1/2. No dobra, to wszystko, co z niej wynika?
Praca nad Kursem Granic idzie mi bardzo sprawnie, myślę, że termin 1.10.2010 jest mocno realny 🙂
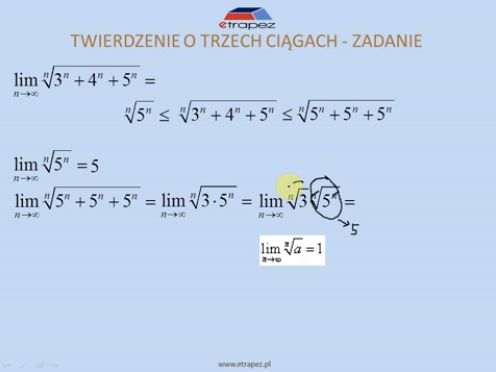
Wklejam na bloga drugi filmik demonstracyjny z Kursu, pokazuję na nim, jak stosować twierdzenie o trzech ciągach do obliczenia granicy, w najbardziej typowym i „oklepanym” na zajęciach typie zadań.
Granice funkcji z sinusem zwykle traktujemy wzorem: x dąży do zera to {sinx}/x=1.
Pytanie: co z cosinusem x? Ma jakąś „typową” granicę?
„Jeżeli w szeregu badania naszego natrafimy na coś, czego nasz umysł dobrze pojąć nie chce, należy się zatrzymać i powstrzymać od dalszego niepotrzebnego badania rzeczy następnych.” KARTEZJUSZ.
Co miał na myśli?
Wirtualny nauczyciel AI działający w przeglądarce internetowej.
