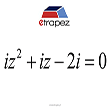
Jak rozwiązać równanie kwadratowe zespolone? (VIDEO)
W filmiku poniżej pokazuję jak rozwiązać równanie kwadratowe zespolone. Okazuje się, że sprawa jest bardzo prosta i nie potrzebujesz wiedzieć zbyt wiele więcej poza wiedzę ze szkoły średniej…
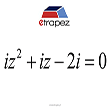
W filmiku poniżej pokazuję jak rozwiązać równanie kwadratowe zespolone. Okazuje się, że sprawa jest bardzo prosta i nie potrzebujesz wiedzieć zbyt wiele więcej poza wiedzę ze szkoły średniej…

Bywają takie dni, w których po prostu nic się nie udaje. Bywają także takie przykłady z liczb zespolonych, w których nic nie idzie. Znane i wykute metody nie pomagają.
Weźmy na przykład taki sobie niewinne potęgowanie: ( 1+2i )^8. Drepcząc wydeptaną już w wielu przykładach ścieżką chcesz zapisać liczbę 1+2i w postaci trygonometrycznej i później podnieść do ósmej potęgi z odpowiedniego wzoru. Ale po drodze napotykasz na komplikacje… Zobacz jaką sztuczkę stosuję.

Wiele równań wielomianowych 4-tego stopnia da się przekształcić na równania kwadratowe znaną dobrze ze szkoły średniej sztuczką z podstawieniem. Działa to oczywiście i jak najbardziej także dla wielomianów w liczbach zespolonych.
Przypatrz się jak zamienić takie równania na równania niższego stopnia.

Przy liczeniu pierwiastków drugiego stopnia w postaci kartezjańskiej (albo: algebraicznej) w moim Kursie Liczb Zespolonych pokazałem pewien patent, polegający na dopisaniu trzeciego równania do układu już dwóch istniejących, co w rezultacie gigantycznie skracało i upraszczało dalsze obliczenia.
Patent pokazałem, ale w żaden sposób nie uzasadniłem. No i właśnie na tą okazję otrzymałem ostatnio maila o treści:
„Czy mógłby Pan wyjaśnić dlaczego możemy użyć patentu na dodanie trzeciego równania podczas obliczania pierwiastka drugiego stopnia z liczby zespolonej?” No to wyjaśniam.

Liczby zespolone jako całość nie są tematem skomplikowanym i trudnym. „Gorąco” może się w nich jednak zrobić w sytuacjach nietypowych i mniej schematycznych. Kluczem jest wtedy – jak zawsze – zrozumienie tematu i „chłodna głowa”, czyli przytomność umysłu i pewność siebie.
Wirtualny nauczyciel AI działający w przeglądarce internetowej.