Asymptoty Wykład 3
Temat: Asymptoty ukośne z funkcji wymiernych
Streszczenie
Mając do wyznaczenia asymptoty z funkcji wymiernych – i tylko z nich – możemy obliczyć asymptoty ukośne (a więc także i poziome) zupełnie bez liczenia granic, a czasami tylko patrząc na funkcję i od razu zapisując odpowiedź. Ponieważ tak się składa, że funkcje wymierne często stanowią obiekt obliczania asymptot, nauka dodatkowych kilku “patentów” może się opłacić.
Przypomnimy sobie najpierw, co to były te funkcje wymierne. Funkcja wymierna to funkcja składająca się z dwóch podzielonych przez siebie wielomianów, tzn.
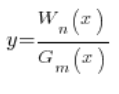– gdzie jako 
i 
przyjąłem sobie stopnie wielomianów.
Mogą to by na przykład funkcje:
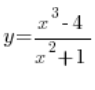(w liczniku mamy wielomian stopnia trzeciego, a w mianowniku drugiego)
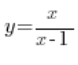(w liczniku i mianowniku mamy wielomiany stopnia pierwszego)
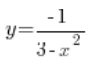(w liczniku mamy wielomian stopnia zerowego, a w mianowniku wielomian stopnia drugiego)
Jak szybko i bez liczenia granic wyznaczyć asymptoty ukośne takich funkcji? Zasady są proste. Wszystko zależy od stopni wielomianów w liczniku i mianowniku. Mamy więc następujące możliwości:
1) Stopień wielomianu w liczniku jest większy o co najmniej 2 od stopnia wielomianu w mianowniku
POSTĘPOWANIE: Asymptoty ukośne nie istnieją. Piszemy to jako odpowiedź. Koniec.
2) Stopień wielomianu w liczniku jest większy o jeden od stopnia wielomianu w mianowniku
POSTĘPOWANIE: Asymptota ukośna istnieje. Dzielimy dwa wielomiany (tak, jak to się w średniej dzieliło), odrzucamy resztę i to co nam wyjdzie to właśnie równanie tej asymptoty ukośnej. Zarówno w 
, jak i w 
. Piszemy odpowiedź. Koniec.
3) Stopień wielomianu w liczniku jest taki sam jak stopień wielomianu w mianowniku
POSTĘPOWANIE: Istnieje asymptota pozioma. Dzielimy współczynniki przy największych potęgach w liczniku i w mianowniku i liczba, która nam wyjdzie to właśnie równanie tej asymptoty poziomej. Zarówno w , jak i w . Piszemy odpowiedź. Koniec.
4) Stopień wielomianu w liczniku jest mniejszy niż stopień wielomianu w mianowniku
POSTĘPOWANIE: Istnieje asymptota pozioma o równaniu 
. Zarówno w , jak i w . Nic nie trzeba już liczyć. Piszemy odpowiedź. Koniec.
Przykłady
Zad. 1
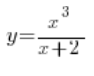
Stopień wielomianu w liczniku (3) jest o 2 większy od stopnia wielomianu w mianowniku (1). Tutaj nie ma asymptot ukośnych.
Zad. 2
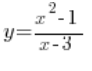
Stopień wielomianu w liczniku (2) jest o 1 większy od stopnia wielomianu w mianowniku (1). Dzielimy wielomiany (tak, jak to się w średniej robiło) i mamy wynik: 
z resztą 
. Piszemy odpowiedź, że prosta 
jest równaniem asymptoty ukośnej przy 
Zad. 3
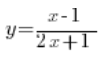
Stopień wielomianu w liczniku (1) jest taki sam jak stopień wielomianu w mianowniku (1). Dzielimy liczby przy największych potęgach w liczniku i w mianowniku i mamy wynik: 
. Piszemy odpowiedź, że prosta 
jest równaniem asymptoty poziomej przy
Zad. 4
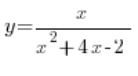
Stopień wielomianu w liczniku (1) jest mniejszy od stopnia wielomianu w mianowniku (2). Piszemy odpowiedź, że prosta jest równaniem asymptoty poziomej przy
Zalety stosowania takich sztuczek są oczywiste (nie trzeba męczyć się z granicami), ale wady chyba również. Po pierwsze, to działa tylko w funkcjach wymiernych (wielomian przez wielomian). W pozostałych trzeba się męczyć standardowymi metodami. Po drugie, trzeba w ogóle umieć dzielić wielomiany, a w dzisiejszych trudnych czasach ta sztuka chyba powoli wymiera (na lipiec 2010 jest jeszcze w programie rozszerzonym matematyki w szkole średniej). Po trzecie, nie wiadomo, jak Twój Pan profesor spojrzy na takie “patenty”. Z drugiej strony widziałem profesorów, którzy uczyli tylko tego i normalnymi granicami nie zaprzątali studentom nawet głowy.
To, czy będziesz więc z tego korzystał, zależy tylko od Ciebie. Powodzenia!
Kliknij, aby przypomnieć sobie, czym są asymptoty ukośne funkcji (poprzedni Wykład) <–
Kliknij, zapoznać się z wybranymi funkcjami mającymi asymptoty (następny Wykład) –>
Kliknij, aby powrócić na stronę z wykładami o badaniu przebiegu zmienności funkcji