Asymptoty Wykład 2
Temat: Asymptoty ukośne – definicja
Streszczenie
Na tym wykładzie zdefiniujemy, czym są asymptoty ukośne funkcji (jako pewnego rodzaju granice niewłaściwe funkcji).
Potrzebne nam będą:
- definicja granicy niewłaściwej funkcji przy
 z poprzedniego Wykładu (Asymptoty Wykład 1)
z poprzedniego Wykładu (Asymptoty Wykład 1)
Co to jest asymptota przy  ? Chłopski rozum
? Chłopski rozum
Na poprzednim wykładzie poznaliśmy asymptoty poziome – były to poziome proste, do których przybliżał się wykres funkcji wraz z rozbieganiem jej argumentów (x) w nieskończoność. Można powiedzieć, że wykres miał asymptotę poziomą, gdy dla argumentów funkcji rozbiegających w ![]() (lub w
(lub w ![]() ) odpowiadające im wartości funkcji zbiegały do jakiejś liczby g, czyli dla
) odpowiadające im wartości funkcji zbiegały do jakiejś liczby g, czyli dla ![]()
![]() .
.
Na wykresie mogło by to wyglądać na przykład tak:
 Mamy więc dwie sprawy: argumenty x rozbiegające w nieskończoność i wykres funkcji przybliżający się do innej krzywej. W naszym przypadku właściwie prostej. Poziomej. 🙂
Mamy więc dwie sprawy: argumenty x rozbiegające w nieskończoność i wykres funkcji przybliżający się do innej krzywej. W naszym przypadku właściwie prostej. Poziomej. 🙂
Nie ma jednak potrzeby, żeby ograniczać się tylko do prostych poziomych jeżeli chodzi o krzywą, do której ma się zbliżać wykres funkcji f(x). Właściwie mogą to być dowolnie proste (niekoniecznie) poziome, albo nawet dowolne inne krzywe. Ważne jest, żeby spełniony był warunek, że wykresy „zbliżają” się do tej krzywej dla argumentów rozbiegających w nieskończoność. Albo innym słowy, żeby dla argumentów rozbiegających w plus/minus nieskończoność odległości pomiędzy wartościami funkcji a wartościami tej krzywej zbiegała do zera.
Pamiętając o tym, że odległość dwóch wartości możemy oznaczyć jako ich różnicę w wartości bezwzględnej, symbolicznie, jeżeli oznaczymy funkcję f(x), a d jako krzywą, warunkiem istnienia asymptoty funkcji przy ![]() będzie:
będzie:

Wniosek z tego taki, że asymptoty takie mogą być tylko dwie, przy ![]() i przy
i przy ![]() .
.
Asymptoty ukośne jako szczególny przypadek asymptot przy  .
.
Skoro asymptoty przy ![]() mogą być dowolną krzywą, no to mogą być i prostą, prawda 🙂
mogą być dowolną krzywą, no to mogą być i prostą, prawda 🙂
I właśnie takie nazwiemy asymptotami ukośnymi. Wyglądała by ona na przykład tak:
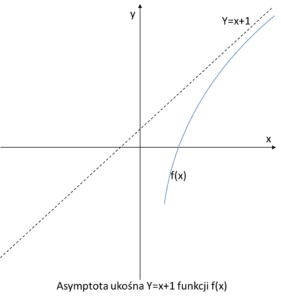 Warunkiem ogólnym istnienia asymptoty jest, przypomnijmy:
Warunkiem ogólnym istnienia asymptoty jest, przypomnijmy:

… gdzie d jest wykresem krzywej, będącej asymptotą. Jeśli umówimy się, że ta krzywa będzie prostą (brzmi śmiesznie, prawda?), to jej równanie ogólne (jak wiemy z gimnazjum) będzie takie: ![]() . co możemy wstawić śmiało za d, uzyskując:
. co możemy wstawić śmiało za d, uzyskując:
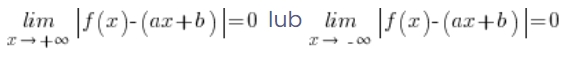
Czyli:

Wartość bezwzględna równa jest zero wtedy i tylko wtedy, kiedy liczona jest z zera (albo – tak jak w naszym przypadku – z czegoś dążącego do zera), zatem:

Po podzieleniu obu stron równania przez x dostaniemy:
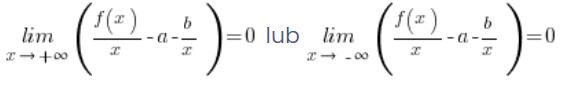
Wyrażenia ![]() w tych granicach dążą do zera (stała przez nieskończoność), zatem powyższe równania będą spełnione, gdy:
w tych granicach dążą do zera (stała przez nieskończoność), zatem powyższe równania będą spełnione, gdy:
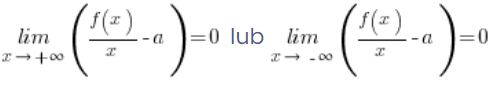
A to będzie z kolei spełnione, gdy:
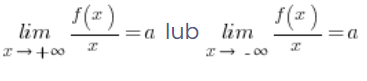
Z drugiej strony widać od razu, że warunek wyjściowy:

Jest spełniony, gdy (przeniosłem b na prawo):
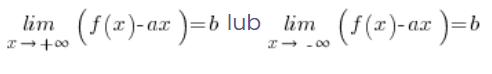
W ten sposób wyprowadziłem konieczne warunki istnienia asymptoty ukośnej. Podsumowując zatem:
Warunki istnienia asymptot ukośnych
Funkcja f(x) osiąga asymptotę ukośną ![]() przy
przy ![]() , gdy:
, gdy:
1. 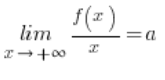
2. 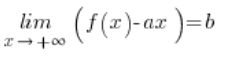
Funkcja f(x) osiąga asymptotę ukośną ![]() przy
przy ![]() , gdy:
, gdy:
1.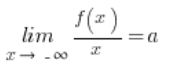
2. 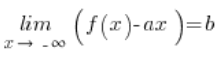
Kliknij, aby przypomnieć sobie, czym są asymptoty pionowe i poziome funkcji (poprzedni Wykład) <–
Kliknij, aby powrócić na stronę z wykładami o badaniu przebiegu zmienności funkcji
