هذا المنشور مخصص للحديث عن جزء من سؤال في امتحان الثانوية العامة، الذي أرسله لي أحد طلاب الثانوية عبر البريد الإلكتروني. من الجيد إلقاء نظرة من باب الفضول وعدم تكرار القول بأن الرياضيات في الجامعة أصعب من الرياضيات المتقدمة في المدرسة الثانوية.
🙂
جزء من السؤال
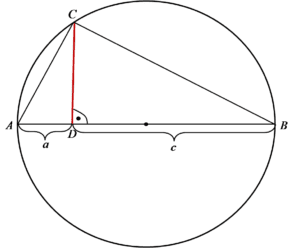
لدينا الحالة التالية:
يجب أن نُظهر أن القطعة المحددة باللون الأحمر لها طول 
. بالطبع هذا فقط جزء صغير من السؤال الكامل، تخمينكم لما يدور حوله؟ إنه حول المتتاليات بالطبع 🙂
لذا يمكننا هنا استخدام حيلة شائعة في مسائل ارتفاع المثلث القائم الزاوية عن طريق الاستفادة من المثلثات المتشابهة التي “يعشقها” جميع طلاب الثانوية.
1. المثلثات 
(الأصغر) و
(الأكبر المدرج في الدائرة) متشابهة (لديهما زاويتان متماثلتان: قائمة و<DAC، مما يعني أن الزاوية الثالثة هي نفسها أيضًا، وهذا يعني أن لدينا تشابه AA). المثلثات 
(المتوسطة) و (الأكبر مرة أخرى) أيضًا متشابهة (لديهما زاويتان متماثلتان: قائمة و<CBD، مما يعني أن الزاوية الثالثة هي نفسها أيضًا، وهذا يعني أن لدينا تشابه AA مرة أخرى). إذا كانت المثلثات: و متشابهة مع ، فإنها أيضًا متشابهة مع بعضها البعض وهذا ما لاحظناه:
مشابه لـ
2. إذا كانت هذه المثلثات متشابهة، فإن نسب الأضلاع المتناظرة ستكون متساوية. بالطبع نختار النسب التي تحتوي على القطعة المحددة باللون الأحمر، والتي سنرمز طولها بـ 
.
في المثلث تكون نسبة الضلع الأقصر إلى الضلع الأوسط متساوية:
في المثلث تكون نسبة الضلع الأقصر إلى الضلع الأوسط متساوية:
بما أن المثلثات متشابهة، فإن هناك مساواة:
3. من هذه المساواة نحدد h، أي طول القطعة المحددة باللون الأحمر. نضرب بالتبادل كما هو الحال في النسب ونحصل على:
يعني:
يعني ما كان علينا أن نثبته في البداية. بينغو.
العبرة هنا هي: عند تحديد الارتفاع في المثلث القائم الزاوية (الذي يسقط على الوتر بالطبع) غالبًا ما نستخدم تشابه المثلثات، كما في الأعلى.
وأيضًا أن الرياضيات المتقدمة في المدرسة الثانوية يمكن أن تكون صعبة حقًا. فقط في الجامعة يمكننا التنفس بسهولة 🙂
