مكان وزمان العمل
حساب المشتقات الاتجاهية كموضوع للدراسة (أي للحصول على العلامة) يأتي فعليًا مباشرة بعد المشتقات الجزئية للدوال متعددة المتغيرات، والتي يدرسها معظم الطلاب في الفصل الدراسي الثاني.
هذا موضوع نادر ما يُتخذ، لذلك لم أدرجه في دورتي عن المشتقات الجزئية، ولكنه شائع بما يكفي لأدرجه في المدونة – لفائدة هؤلاء الذين يحتاجون لتعلم المشتقات الاتجاهية وأولئك الذين هم ببساطة فضوليون لمعرفة ما الأمر. ولكن، كما في الدورات، سأركز اليوم تقريبًا فقط على التطبيق („كيف أفعل هذا؟”) وليس على النظرية („ماذا أفعل بالضبط؟”).
المشتقات الاتجاهية – كيف أفعل هذا؟
في حالة المشتق الاتجاهي، نحن نتعامل مع زيادة متزامنة في المتغيرين x و y، وهو ما يقابله بالطبع زيادة في قيمة الدالة ![]() .
.
لحل المسألة نحتاج إلى ثلاث أشياء:
- دالة نحسب منها المشتق الاتجاهي.
- نقطة نحسب عندها المشتق الاتجاهي.
- اتجاه معطى في شكل متجه.
عند توفر هذه الأشياء، تتلخص المسألة في تحويل المتجه إلى متجه اتجاهي (شيء من الهندسة التحليلية، سأريكم كيف نفعل ذلك بعد قليل)، ثم إدخاله في الصيغة:
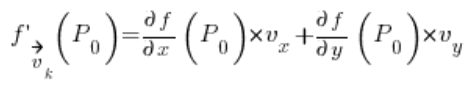
حيث أن:
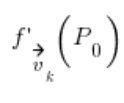 هو المشتق الاتجاهي في النقطة
هو المشتق الاتجاهي في النقطة ![]() في اتجاه المتجه
في اتجاه المتجه ![]()
![]() هي النقطة التي نحسب عندها المشتق الاتجاهي
هي النقطة التي نحسب عندها المشتق الاتجاهي
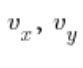 هي إحداثيات المتجه الاتجاهي
هي إحداثيات المتجه الاتجاهي
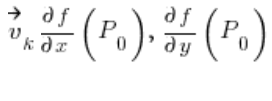 هي المشتقات الجزئية للدالة
هي المشتقات الجزئية للدالة ![]() في النقطة
في النقطة ![]() .
.
احسب المشتق الاتجاهي للدالة 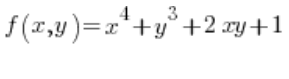 في النقطة P(1,2) في الاتجاه
في النقطة P(1,2) في الاتجاه 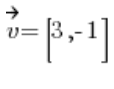 .
.
الحل:
كل شيء جاهز، فقط يجب تحويل المتجه 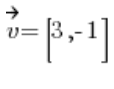 إلى متجه اتجاهي.
إلى متجه اتجاهي.
المتجه الاتجاهي هو متجه بنفس الاتجاه (من كان ليظن ذلك)، وبنفس الاتجاه، ولكن بطول 1.
يتم حسابه بالصيغة:
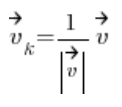
بمعنى بسيط، قسمة إحداثياته على طوله.
لذلك نحسب طول المتجه ![]() :
:
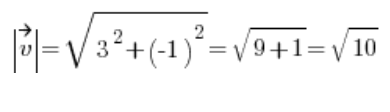
ثم نحصل على المتجه الاتجاهي:
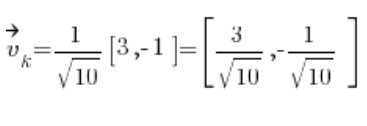
في الصيغة الخاصة بالمشتق الاتجاهي، نحتاج إلى المشتقات الجزئية للدالة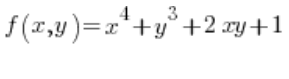 في النقطة P(1,2):
في النقطة P(1,2):
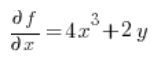
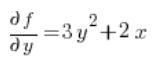
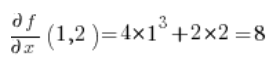
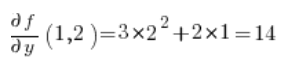
والآن لدينا كل ما نحتاجه للصيغة:
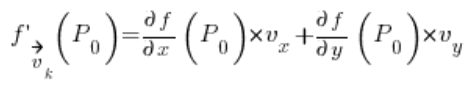
نقوم فقط بالإدخال ولدينا النتيجة: 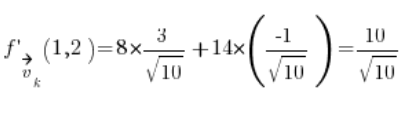 .
.
تم.
المثال 2
ابحث عن المشتق الاتجاهي للدالة: 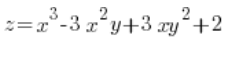 في النقطة P(3,1) في الاتجاه من هذه النقطة إلى النقطة Q(6,5).
في النقطة P(3,1) في الاتجاه من هذه النقطة إلى النقطة Q(6,5).
الحل:
المسألة أكثر صعوبة قليلاً لأن المتجه الاتجاهي غير معطى مباشرة، ولكن لا مشكلة.
ننتقل من النقطة P إلى النقطة Q، فيكون المتجه الانتقالي هو المتجه [3,4].
الآن نبحث عن المتجه الاتجاهي بحساب طول المتجه [3,4]:
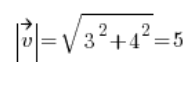
ونحصل على المتجه الاتجاهي:
الآن نحسب المشتقات الجزئية في النقطة (3,1):
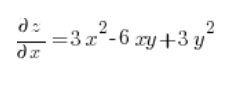
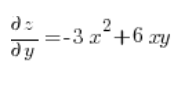
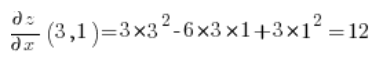
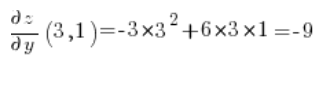
ونقوم فقط بالإدخال في الصيغة الخاصة بالمشتق الاتجاهي:
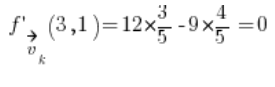
المثال 3
ابحث عن المشتق الاتجاهي للدالة 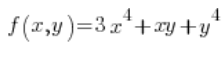 في النقطة (1,2) في الاتجاه الذي يكون زاوية
في النقطة (1,2) في الاتجاه الذي يكون زاوية ![]() مع المحور X الموجب.
مع المحور X الموجب.
الحل:
المسألة تبدو أصعب، بسبب عدم وجود متجه الاتجاه في المعطيات. دعونا نرسم الأمر:

الأمر يتعلق بإيجاد إحداثيات أي متجه في الاتجاه المعين.
نستخدم حقيقة أن 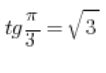 ويمكننا افتراض أن متجهنا له الإحداثيات
ويمكننا افتراض أن متجهنا له الإحداثيات 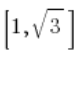 ، كما هو في الرسم (كان يكفي اختيار أي متجه في اتجاه الخط):
، كما هو في الرسم (كان يكفي اختيار أي متجه في اتجاه الخط):

والآن نقوم بالطريقة المعتادة.
نحسب المتجه الاتجاهي:
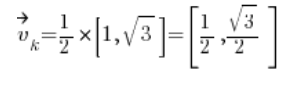
ثم المشتقات الجزئية في النقطة (1,2):
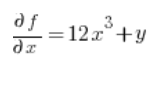
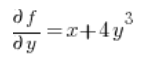
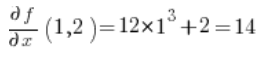
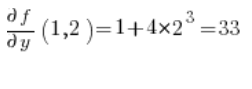
نقوم بالإدخال في الصيغة ولدينا النتيجة
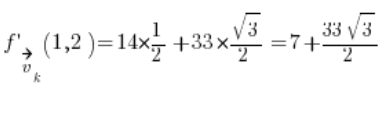
أرحب بأسئلتكم في التعليقات – كالعادة 🙂


