من أين جاء هذا الاختراع في الجذور المركبة؟ من أين أتى المعادلة الثالثة عند حساب الجذر التربيعي لعدد مركب؟

عند حساب الجذور التربيعية في الشكل الكارتزي (أو: الجبري) في دورتي حول الأعداد المركبة، أظهرت طريقة تعتمد على إضافة معادلة ثالثة إلى النظام المكون من معادلتين موجودتين بالفعل، مما يؤدي إلى تبسيط وتقصير العمليات الحسابية بشكل كبير.

عرضت هذه الطريقة ولكن لم أبررها بأي شكل من الأشكال.

ومؤخرًا تلقيت رسالة بريد إلكتروني بهذه المناسبة تقول:

مرحبًا

هل يمكن أن تشرح لماذا يمكننا استخدام الطريقة بإضافة معادلة ثالثة عند حساب الجذر التربيعي لعدد مركب؟

x^2 + y^2 = قدر العدد الذي نحسب جذره

هذا سؤال ممتاز جدًا، ومبارك على كل من في الرياضيات الذين لا يصدقون الأساتذة على الفور، بل يسألون دائمًا: “من أين أتى هذا؟” 🙂

التبرير

إذاً لم يبق لي إلا أن أبرر هذه الطريقة بإحدى الطرق الممكنة:

بعد بضعة خطوات في حساب الجذر التربيعي نصل إلى الحالة التالية:

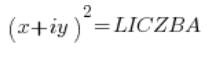
نظرًا لأن الأعداد (لن أقول “الأعداد المركبة” في كل مرة) على اليسار واليمين متساوية، فإن مقاديرها أيضًا يجب أن تكون متساوية (العكس غير صحيح، ولكن هذا غير مهم)، أي:

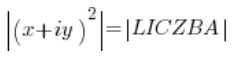
العدد المربع هو العدد مضروبًا في نفسه، أي:

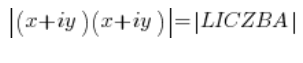
قدر العدد المركب له خاصية: ، أي على الجانب الأيسر يمكننا كتابة:

… وعند حساب المقادير على الجانب الأيسر نحصل على:

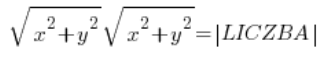
أي:

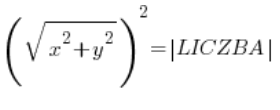
أي:

أي:

بِنغو

شكرًا على السؤال الجيد!