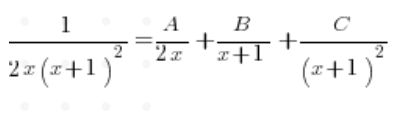دلتا تساوي صفر في تكاملات غير محددة جذرية
Krystian Karczyński
مؤسس ورئيس موقع eTrapez.
حاصل على درجة الماجستير في الرياضيات من الجامعة التقنية في بوزنان (بولندا). معلم خصوصي للرياضيات بخبرة عديدة سنوات. مبتكر أول دورات eTrapez، التي حققت شعبية كبيرة بين الطلاب في جميع أنحاء بولندا.
يعيش في شتشيتسين (بولندا). يحب النزهات في الغابة، الاستجمام على الشاطئ، وركوب الكاياك.
تحليل المعادلة التربيعية إلى عوامل
في التكاملات غير محددة الجذرية يحدث (غالباً) الحاجة إلى تحليل المعادلة التربيعية إلى عوامل: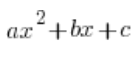 
. نفعل ذلك بالطبع من خلال الصيغة: 
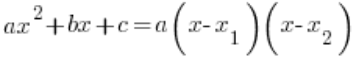, والتي تعمل عندما 
.
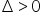التكاملات الجذرية ودلتا تساوي 0
لكن كيف يبدو الثنائي، عندما تكون دلتا 0؟ مثلاً كيف سيبدو: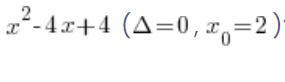 
في صورة عوامل؟
هل هكذا: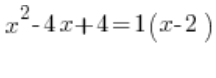 
؟
بالطبع لا… من المدرسة الثانوية نتذكر أن إذا 
فإننا في الواقع نجد جذرًا واحدًا، ولكنه جذر مزدوج. لذلك في مثالنا يمكننا القول: 
، أي أن المعادلة التربيعية تُفكك إلى عوامل بالشكل التالي:
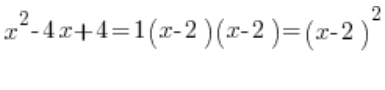
وهذا له عواقب كبيرة في التكاملات غير محددة الجذرية عند فكها إلى كسور بسيطة.
مثال
لنأخذ مثالاً:
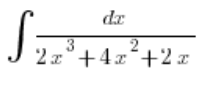
نقوم بفك الكسر بشكل منفصل بدون التكامل، مما يعني:
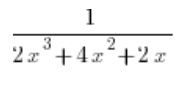
نقوم بإخراج x من المقام:
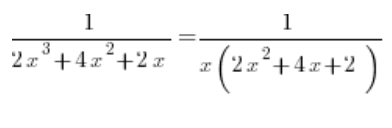
نحسب الدلتا من المعادلة التربيعية في الأسفل، نحصل على 0، والجذر هو -1. وبالتالي، بفكها إلى عوامل نحصل على:
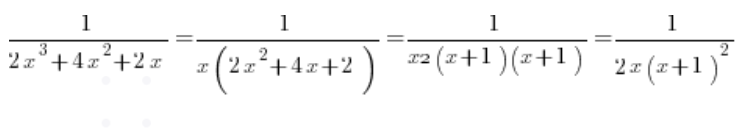
ولفكها إلى كسور بسيطة:
هل تبحث عن دروس خصوصية في الرياضيات لمستوى الجامعة أو المدرسة الثانوية؟ أو ربما تحتاج إلى دورة تحضيرية لاختبار الثانوية العامة؟
نحن فريق eTrapez. نعلم الرياضيات بطريقة واضحة، بسيطة ودقيقة جدًا - سنصل حتى إلى الأكثر مقاومة للمعرفة.
لقد قمنا بإنشاء دورات فيديو بلغة مفهومة يمكن تحميلها على الكمبيوتر، الجهاز اللوحي أو الهاتف. تشغل التسجيل، تشاهد وتستمع، كما لو كنت في دروس خصوصية. في أي وقت من اليوم أو الليل.
