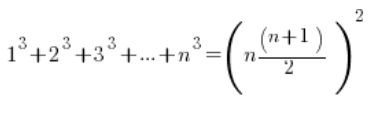في حدود المتتاليات، أحيانًا تكون هكذا:
وأحيانًا تكون هكذا:
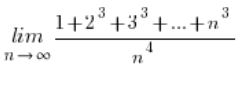
ماذا نفعل حينها؟
الجواب بسيط:
الصيغ لمجموع المربعات ومجموع المكعبات للأعداد الطبيعية المتتالية.
الصيغ كانت كالتالي:
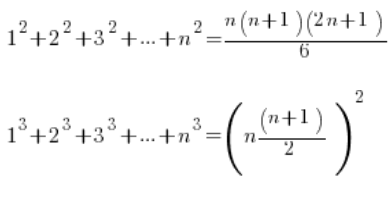
الصيغ – كأي صيغ – لحفظها عن ظهر قلب. إذا كنت قد واجهت أمثلة مماثلة وتحتاجها بالفعل.
بمعرفة هذه الصيغ يصبح حساب الحدود الخاصة بنا سهلاً للغاية:
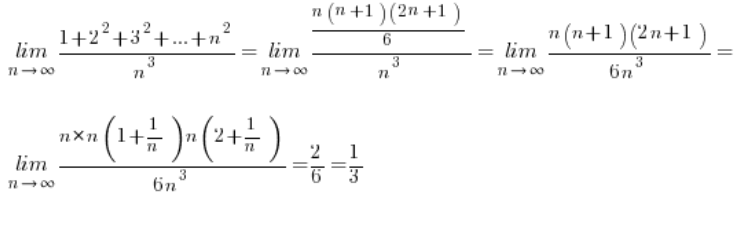
الحد التالي:
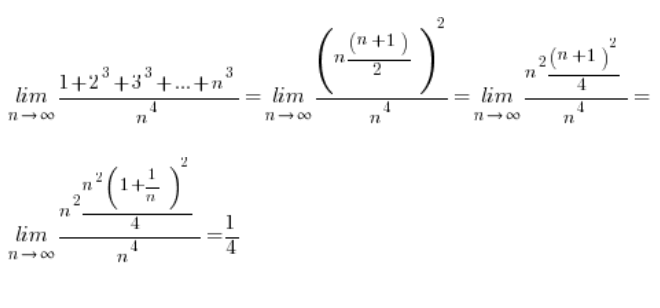
البراهين الاستقرائية للصيغ
يمكن إثبات صحة الصيغ بسهولة نسبية باستخدام الاستقراء (على الأقل قبل بضع سنوات كان هذا معيارًا في المدرسة الثانوية). سأقوم بذلك للصيغة التالية:
1. 
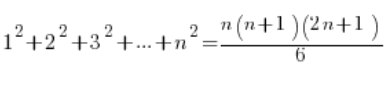
الخطوة الاستقرائية الأولى
نتحقق من صحة الصيغة عندما n=1:
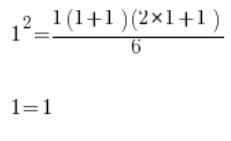
صحيح
الخطوة الاستقرائية الثانية
نفترض الفرضية، أنه بالنسبة لعدد طبيعي معين n:
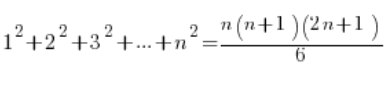
الخطوة الاستقرائية الثالثة
نثبت النظرية (باستخدام الفرضية المفترضة) أنه بالنسبة ل n+1 فإن الصيغة تنطبق أيضًا، أي:
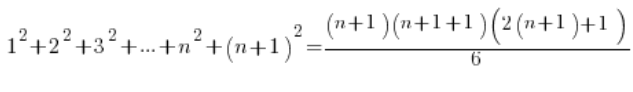
على الجانب الأيسر بدلاً من 
نضع الصيغة من الفرضية، وعلى الجانب الأيمن نقوم بالترتيب فقط:
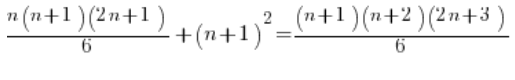
ثم بدلاً من العمل بشكل متعجل نتصرف بدقة أكبر:
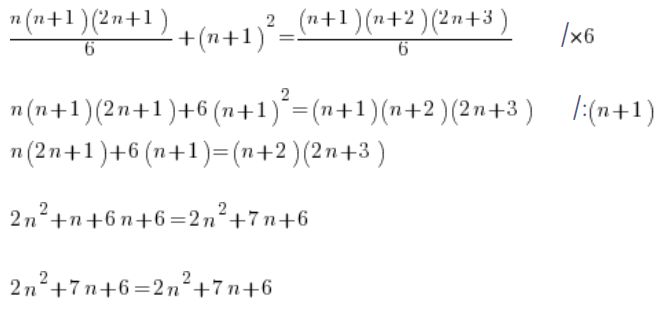
أي أن النظرية قد ثبتت. الصيغة قد ثبتت بالاستقراء.
أدعوكم لإثبات الصيغة الثانية بالاستقراء، لمجموع المكعبات:
