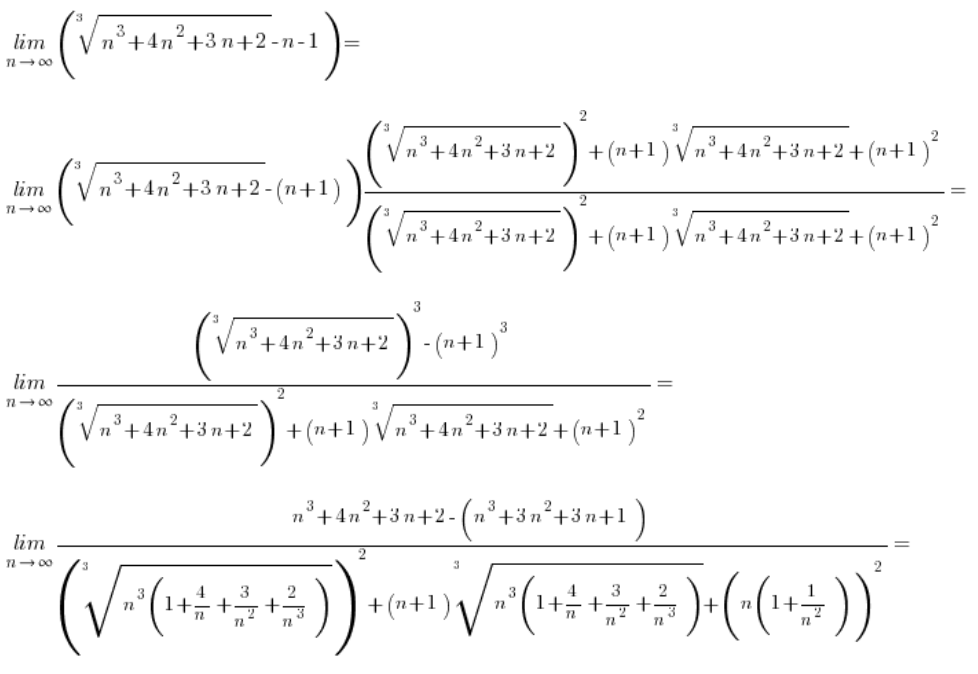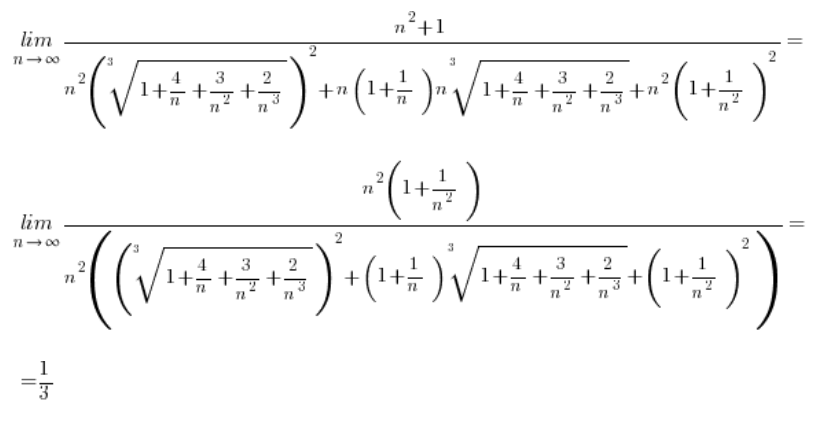كيف كان الأمر مع الجذور “العادية”؟
عندما كان لدينا حد لحسابه، وكان هناك نوع من الطرح مع الجذر (والذي لم يكن يمكن حسابه بشكل أبسط، بالطبع)، يعني:
“شيء – جذر لشيء”
“جذر لشيء – شيء”
“جذر لشيء – جذر لشيء”
كنا نستخدم خدعة أسميها – “الضرب بالمرافق”.
ببساطة، كنا نضرب هذا التعبير بنظيره مع علامة الجمع، أو بالأحرى بكسر يحتوي على هذا النظير في البسط والمقام.
على سبيل المثال:
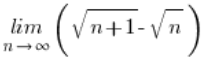كنا نضرب هكذا: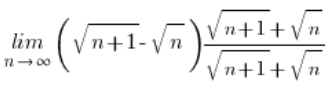 
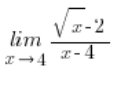كنا نضرب هكذا: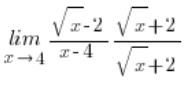 
هذه الخدعة الذكية كانت تسمح لنا بالخروج إلى نمط ضرب مختصر:
بعد الخروج إلى هذا النمط، كانت المربعات “تقصي” الجذور وكنا نخرج إلى النتيجة البسيطة (حسناً، نقول أحياناً بسيطة أطول قليلاً).
ولكن ماذا عن الحالة عندما تكون الجذور متورطة في الطرح من الدرجة الثالثة؟ مثل هنا على سبيل المثال:
\underset{x\to 8}{\mathop{\lim }}\,\frac{\sqrt[3]{x}-2}{x-8}الطريقة القياسية للإجراء، أي الضرب على النحو التالي:
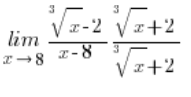
لن تعطينا شيئًا، لأن هذه المرة في البسط بعد الخروج إلى النمط:
المربعات لن “تقصي” الجذور من الدرجة الثالثة بأي شكل من الأشكال. يعني سنظل في نفس النقطة.
كيف سيكون الأمر مع الجذور من الدرجة الثالثة؟
في حالة الطرح مع الجذور من الدرجة الثالثة، يجب ببساطة “التوجه” إلى نمط مختلف تمامًا (ولكن من المدرسة الإعدادية أيضًا)، وهو:
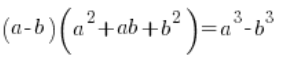
يعني بياناتنا 
(حيث a أو b أو كلاهما جذور من الدرجة الثالثة) بدلاً من ضربهما بـ 
سنضربهما بـ 
وبعد تطبيق النمط، ستقوم المكعبات بعملها، “مقصية” الجذور.
مثال 1
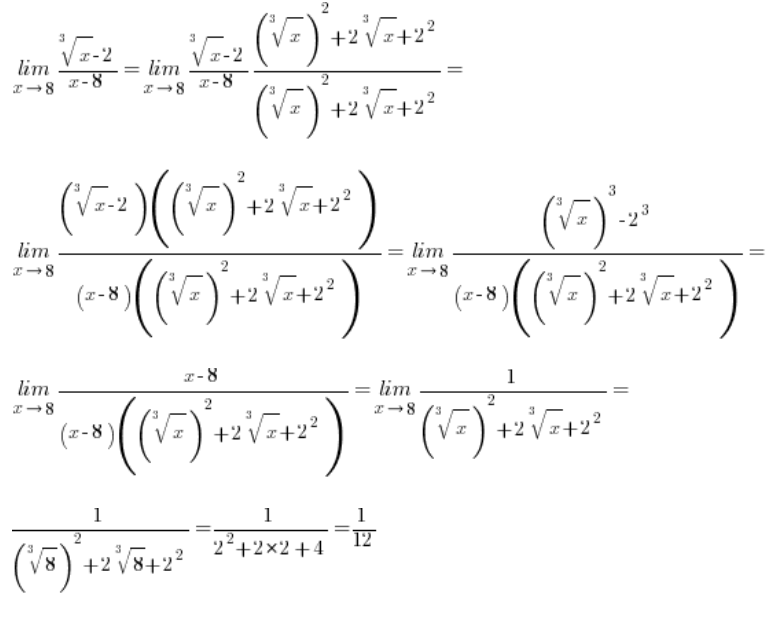
مثال 2
