تبديل أويلر من النوع الأول (للـ a>0) – المراجعة
في المنشور السابق:
تعاملنا مع تكاملات من النوع:
 ,
,
حيث a>0.
قمنا أيضًا بحل تكامل نموذجي يفي بهذا الشرط، أي
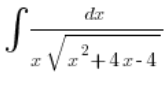
ماذا لو كان ![]() في ثلاثية الحدود سالبًا (حالة a=0 يمكن تجاهلها لأنه لن يكون لدينا ثلاثية حدود مربعة وسنقوم بحل التكامل باستخدام تبديل أبسط
في ثلاثية الحدود سالبًا (حالة a=0 يمكن تجاهلها لأنه لن يكون لدينا ثلاثية حدود مربعة وسنقوم بحل التكامل باستخدام تبديل أبسط ![]() من تبديل أويلر) ؟
من تبديل أويلر) ؟
في هذه الحالة، يمكن أن يساعدنا (أو لا يساعدنا…) النوع الثاني من تبديل أويلر:
تبديل أويلر من النوع الثاني (للـ c>0)
لدينا تكامل من النوع:
 ,
,
حيث c>0، نستخدم التبديل من النوع:
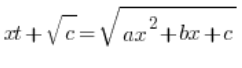 ,
,
نرفع كلا الجانبين إلى المربع، حيث تتبسط المكونات مع ![]() وعلينا أن نقسم كلا الجانبين على
وعلينا أن نقسم كلا الجانبين على ![]() للوصول إلى علاقة خطية، من خلالها نستطيع تحديد
للوصول إلى علاقة خطية، من خلالها نستطيع تحديد ![]() بالتسلسل:
بالتسلسل:
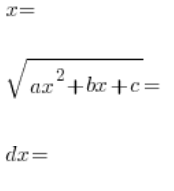
نضع هذا كله في التكامل:

وسنصل مجددًا إلى تكامل نسبي، الذي – كما أكرر – عادةً ما يكون شاقًا.
لنبدأ بالمثال.
مثال
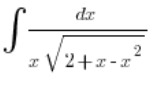
في ثلاثية الحدود تم تغيير ترتيب المكونات قليلاً، ولكن من الواضح أن ![]() . مما يعني أن
. مما يعني أن ![]() ليس أكبر من
ليس أكبر من ![]() (لذلك لن نستخدم النوع الأول من تبديل أويلر)، ولكن c>0 (لذلك سنستخدم النوع الثاني).
(لذلك لن نستخدم النوع الأول من تبديل أويلر)، ولكن c>0 (لذلك سنستخدم النوع الثاني).
نقوم بالتبديل:
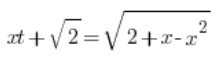
نرفع كلا الجانبين إلى المربع:
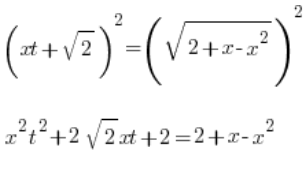
المكون 2 يتبسط (وهذا ما يجب أن يحدث):
![]()
والآن نقسم كلا الجانبين على x:
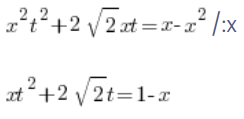
ثم نحسب x:
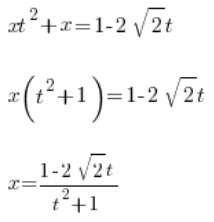
قمنا بحساب x باستخدام المتغير t. الآن نحسب 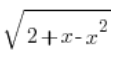 . في البداية لدينا التبديل:
. في البداية لدينا التبديل:
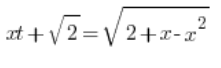
![]() قد تم حسابه، لذا فقط نضعه:
قد تم حسابه، لذا فقط نضعه:
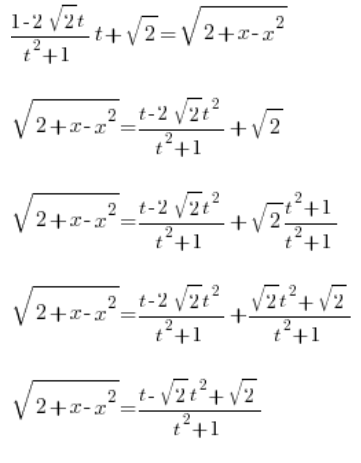
نحتاج الآن فقط لحساب ![]() . نحسبه بأخذ المشتقة من
. نحسبه بأخذ المشتقة من ![]() :
:
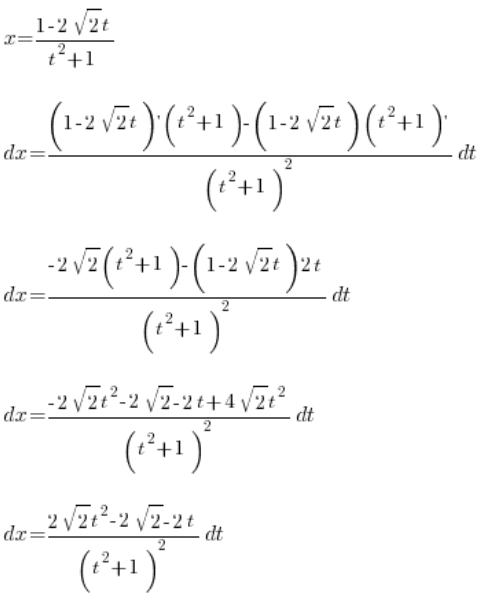
لقد قمنا بحساب:
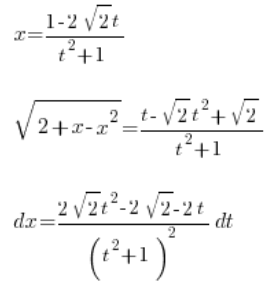
، كل ذلك باستخدام المتغير ![]() . نأخذ التكامل:
. نأخذ التكامل:
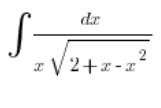
ونضع:
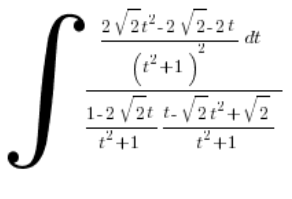
نبدأ في التنظيف:
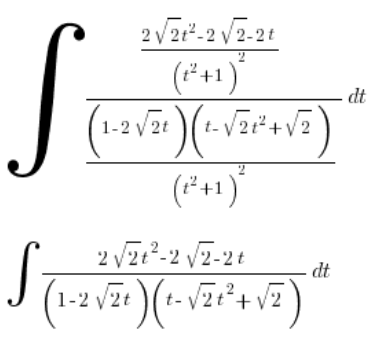
نعود إلى التبديل:
\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+Cنحتاج أيضًا للعودة من t إلى x. كان تبديلنا لأويلر
xt+\sqrt{2}=\sqrt{2+x-{{x}^{2}}}منه
t=\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x}وبالتالي فإن الحل لدينا
\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x} \right|+Cماذا عن الحالات الأخرى؟
نعلم أنه عندما يكون لدينا تكامل:

- a>0 – نستخدم النوع الأول من التبديلات
- c>0 – نستخدم النوع الثاني من التبديلات
ماذا إذا لم يكن أي من ![]() ولا
ولا ![]() أكبر من الصفر؟ سنناقش هذا في المنشور التالي، حيث سنتناول النوع الثالث من تبديل أويلر وسنوضح أن الموضوع سيكون قد انتهى، أي أن كل تكامل من النوع:
أكبر من الصفر؟ سنناقش هذا في المنشور التالي، حيث سنتناول النوع الثالث من تبديل أويلر وسنوضح أن الموضوع سيكون قد انتهى، أي أن كل تكامل من النوع:

… سنختار له أحد أنواع التبديل الثلاثة.


