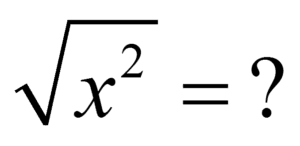اليوم سأكون قصيرًا جدًا. سؤالي السريع لك هو:
كم هو جذر x تربيعًا؟
أي:
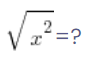
عندما كنت أعطي دروس خصوصية، طرحت هذا السؤال على العديد من الطلاب في المدارس الثانوية والجامعات. هل تعرف كم عدد من عرفوا الإجابة الصحيحة؟
اثنان.
كانت إحصائية الإجابات كالتالي:
75% قالوا أن 
(إجابة خاطئة)
20% شعروا بالفخ وخافوا من الإجابة
5% اخترعوا أشياء غريبة ومفاجئة
أتجاوز عن حالتي الطلاب الذين عرفوا الإجابة الصحيحة (وهؤلاء يعودون إلى 7-8 سنوات من الدروس المكثفة).
الإجابة
حقًا لا أعرف لماذا لا يعرف أحد هذا، لكن الجذر التربيعي لـ x تربيعًا هو القيمة المطلقة لـ x:
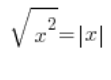
لو كان الجذر هو x، أي لو كان:
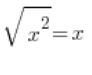
هذا يعني أنه إذا أخذنا (-1) لـ x، يجب أن نحصل على:
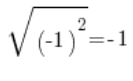
…ولكنا لا نحصل على هذا، بل نحصل على:
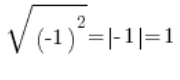
ستواجه هذا الفخ مرارًا في الجامعة، ويجب أن تكون يقظًا. لم أسأل طلابي من أجل إجراء استطلاعات خاصة (في الوقت الذي كانوا يدفعون لي فيه)، بل لأن هذا السؤال كان يظهر في سياق مواضيع مختلفة.
حسنًا، ولكن لماذا هذا؟ – مثال
في حدود الدوال (وسلاسل الأعداد أيضًا)، يجب أحيانًا استخدام هذا الخدعة:
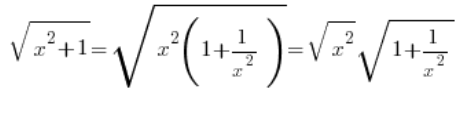
…والخطأ الشائع هنا هو:
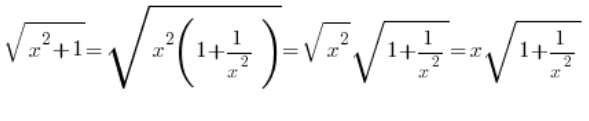
…وهذا قد يكون صحيحًا، أو قد لا يكون صحيحًا، لأنه ينبغي أن يكون:
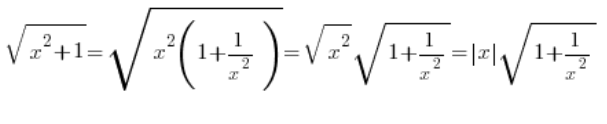
…الآن يجب علينا التحقق مما إذا كان x موجبًا أم سالبًا (إذا كنا في الحدود ونعلم على سبيل المثال أن 
، فإننا نعلم أنه موجب وبشدة).
باستخدام تعريف القيمة المطلقة:
…نعلم أنه إذا كان x موجبًا (حسنًا: غير سالب) ، فإن:
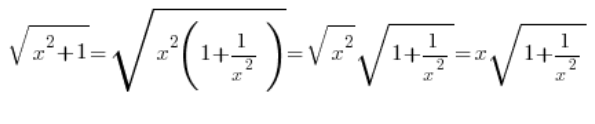
…لكن إذا كان x سالبًا، فإننا نفاجأ بأن:
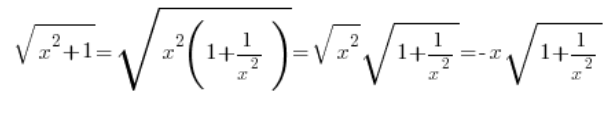
الخطأ بالطبع يؤثر غالبًا على النتيجة النهائية وعلى درجات الامتحان.
لذا احذر من 
!
