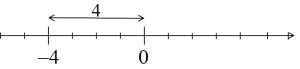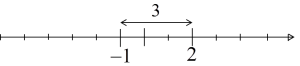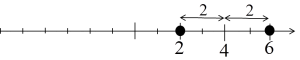بعض الأشياء التي يجب أن تتعلمها جيدًا في المدرسة الثانوية ولكن لم يخبرك بها أحد – الجزء 1 القيم المطلقة

---

إذا كنت تدرس الرياضيات في الجامعة منذ فترة، فلا شك أنك لاحظت أن معظم المواد التي تمت دراستها في المدرسة الثانوية لا تفيدك مباشرة في الجامعة. إذا كنت قد بدأت للتو في التعلم – انتبه إلى هذا.

ماذا يعني “مباشرة”؟

أقول “مباشرة” لأن كل قطرة من عرقك الرياضي في المدرسة الثانوية لن تذهب سدى وستحسب لك. أتحدث عن التدريب على التفكير المجرد، والقدرة على التركيز على المشكلة وما إلى ذلك.

ومع ذلك، بصراحة، لن تحتاج إلى العودة إلى العديد من فروع الرياضيات التي تمت دراستها في المدرسة الثانوية، حتى لإلقاء نظرة سريعة عليها.

لكن هناك استثناءات.

هناك أشياء، إذا لم تتعلمها في المدرسة الثانوية، فلن تتمكن من التقدم في الجامعة.

في بداية العام الدراسي، يجدر بك مراجعتها أو تعلمها. بفضل هذا، ستفتح الطريق أمام نفسك لمزيد من المفاهيم الجديدة. إذا لم تتم دراستها، فستظل تزعجك، مما يعيق (أو حتى يمنع) تقدمك.

لن تكون هذه الفروع الكبيرة للرياضيات، بل ستكون غالبًا تفاصيل صغيرة، قطع صغيرة من البناء التي يمكن أن تنهار بدونه.

تعريف الحد

خذ على سبيل المثال تعريف حد التسلسل الذي ستواجهه قريبًا:

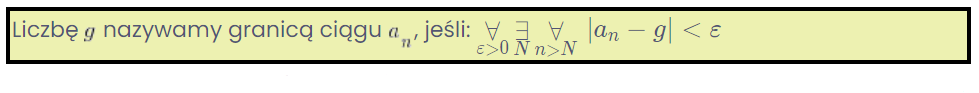
هل تفهم هذه الرموز الغريبة على اليسار؟ وماذا عن القيمة المطلقة على اليمين؟ ليس كثيرًا؟

ومع ذلك، لفهم أو حتى قراءة هذا التعريف بشكل صحيح، يجب أن تكون على دراية بالكمية (هذه الكائنات على اليسار: ) والتفسير الهندسي للقيمة المطلقة (على اليمين) من المدرسة الثانوية…

لكن دعونا لا نتذمر، بل نبدأ العمل. في هذه المنشورات واللاحقة، سأعرض عليك بعض التفاصيل التي سيسهل فهمها الدراسة الجامعية بشكل كبير.

نبدأ من…

1. التفسير الهندسي للقيمة المطلقة (كالمسافة)

ما يتعلق بالقيمة المطلقة هو أننا جميعًا نعرف تقريبًا. لا أحد لديه مشكلة مع حقيقة أن:

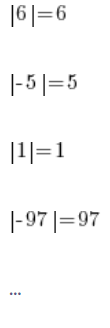
عملية القيمة المطلقة تعيد فقط نفس الرقم، وإذا كان سلبيًا، فإنها تغير العلامة إلى موجب.

ماذا تعني هندسيًا؟ على المحور العددي؟ إنها ببساطة مسافة الرقم عن الصفر. على سبيل المثال، 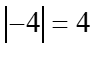ومن المؤكد أن مسافة الرقم عن الصفر هي 4:

سنلتزم بهذا الخط ونفهم القيمة المطلقة كـ مسافة.

لاحظ شيئًا آخر:

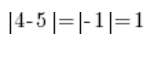
وكذلك، على المحور العددي:

…بمعنى أن المسافة بين 4 و 5 تساوي القيمة المطلقة للفرق (الطرح) بين 4 و 5، بغض النظر عما نطرحه من ماذا، لأن:

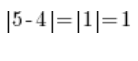
بنفس الطريقة، إذا طرحنا الأعداد 3 و 8 وأخذنا القيمة المطلقة للنتيجة، سنحصل على المسافة على المحور العددي بين الأعداد 3 و 8 (ستكون 5).

يعمل هذا أيضًا مع الأعداد السالبة، مثل -1 و 2:

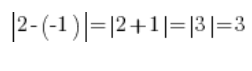
…وهذا يعني المسافة بين الأعداد -1 و 2:

يمكنك أيضًا اللعب بهذا قليلاً بنفسك. إذا كان لديك كتاب مدرسي من المدرسة الثانوية، أشجعك بشدة على أن تجلس لمدة ساعة على هذا الموضوع وتستكشفه قليلاً.

يمكننا صياغة قاعدة عامة:

القيمة المطلقة للفرق (الطرح) بين عددين: و تساوي المسافة بين هذه الأعداد.

كيف يمكننا فك شفرة معادلة مثل:

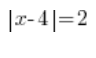
نعلم أن الجزء يعني مسافة المجهول x من 4، وعلى الجانب الأيمن من المساواة نعلم أن هذه المسافة يجب أن تكون تساوي 2.

لذلك، فإن حل المعادلة سيكون الأعداد التي تكون مسافتها عن 4 تساوي 2، وهي الأعداد 2 و 6:

والآن دعونا نأخذ هذا المتباينة:

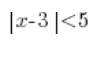
الجانب الأيسر منها هو مسافة x عن الرقم 3، وبقراءة البقية نحصل على المعلومات أن هذه المسافة يجب أن تكون أقل من 5. هذه المرة، لن يكون حل هذه المتباينة عددين فقط بل الكثير – كل الأعداد التي تكون مسافتها عن 3 أقل من 5. على المحور، سيبدو هذا كما يلي:

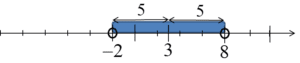
…بمعنى أنها ستكون كل الأعداد من -2 إلى 8، أي الفاصل العددي: . المسافة بين كل هذه الأعداد والرقم 3 أقل من 5.

يمكن أيضًا تسمية هذا الفاصل العددي ب الجوار من النقطة 3 (مصطلح مهم، يستخدم كثيرًا في الجامعة).

بتفكير بنفس الطريقة، يمكنك اكتشاف الأعداد التي تحقق المتباينة …

ولكن ليس هذا هو هدفي (وأنت قد تعلمت هذا بالفعل في المدرسة الثانوية، أليس كذلك؟).

من الجيد فهم القيمة المطلقة كمسافة، لأنها تظهر في العديد من التعريفات الرياضية التي ستواجهها في الجامعة. وبالتالي، من الجيد أن تعرف مباشرة “ما الذي يجري”.

خذ على سبيل المثال الحد الذي تمت مناقشته سابقًا:

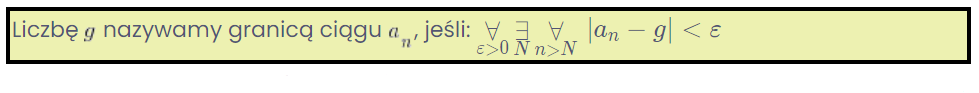
لنركز في الوقت الحالي على الجانب الأيمن من المعادلة. دعونا نترك الرموز الغريبة على اليسار للمنشور التالي.

أي من التفسيرات التالية أقرب إلى القلب وأسهل في الفهم:

“القيمة المطلقة للفرق و يجب أن تكون أقل من ”

أو:

“المسافة بين و يجب أن تكون أقل من ”

؟

بشكل رسمي، كلا الطريقتين في صياغة التعريف متكافئتين، لكن الطريقة الثانية أبسط وتركز على الجوهر دون تشتيت بالعمليات الحسابية.

فهم القيمة المطلقة كمسافة سيساعدك كثيرًا على فهم العديد من النظريات والتعريفات الرياضية – التي تبدو معقدة – في الجامعة.

ماذا بعد؟

في المنشور التالي، سأتعامل مع هذه الرموز الغريبة: و ، حتى نتمكن من فهم تعريفنا المثال بالكامل.