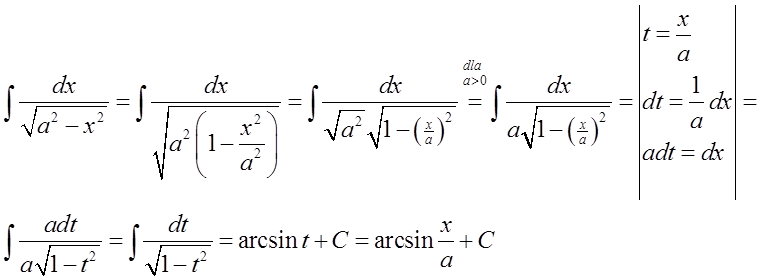القواعد المحرمة للتكاملات غير المحددة – اشتقاق القواعد

---

أساتذة الجامعات لديهم متطلبات خاصة بهم. العديد منهم – من أجل مصلحة طلابهم بالطبع – لن يتراجعوا عن تحديد قواعد دقيقة لكيفية حل المسائل.

أحد مستخدمي دورة التكاملات غير المحددة كتب لي على GG ما يلي:

لدي طلب، هل يمكنك على صفحتك على الفيسبوك أو مدونتك أن تظهر كيف يتم تحويل التكاملات في صيغك إلى الشكل الموجود على الورقة؟ أقصد الصيغ أرقام: 5, 9, 10, 13, 14, 15, 16. للأسف لدينا الأستاذة أخبرتنا أنه يمكن استخدام الصيغ الأبسط فقط، أما الصيغ الأكثر تعقيداً التي ذكرتها يجب علينا تفكيكها بأنفسنا إلى الشكل المعطى. أعتقد أن العديد من الأشخاص سيكونون ممتنين لك 🙂

يتعلق الأمر بالورقة التي تحتوي على الصيغ المرفقة بـالدورة:

صيغ التكاملات غير المحددة

وتحديداً الصيغ:

5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}

 

9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}

 

10.\quad \int{ctgxdx=\ln \left| \sin x \right|}+C

 

13.\quad \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}

 

14.\quad \int{\frac{dx}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{2a}\ln \left| \frac{x-a}{x+a} \right|+C}

 

15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}

 

16.\quad \int{\frac{dx}{\sqrt{{{x}^{2}}+q}}=\ln \left| x+\sqrt{{{x}^{2}}+q} \right|+C}

 

إذا لم تكن هذه الصيغ، فبالتأكيد صيغ أخرى

نعم، هذا صحيح، الأساتذة غالباً ما يطلبون استخدام صيغ محددة فقط، أو عدم استخدام بعضها نهائياً. أو ربما يطلبون استخدام صيغ نحن لا نحب استخدامها.

الطريقة الوحيدة للعقلاء في مثل هذه الحالات هي الامتثال الكامل. في قاعة الامتحان، الأستاذ هو القانون ولا فائدة من الشكوى لاحقاً للأصدقاء أن الأستاذ لم يقبل الامتحان، رغم أنه “كان يجب عليه”.

بدلاً من ذلك، سأقوم بمراجعة الصيغ المذكورة واحدة تلو الأخرى وأوضح كيفية التعامل مع كل حالة بشكل فردي (للأسف لا يمكن شمولها جميعاً بقاعدة واحدة). “التعامل” يعني حل التكاملات التي تتطلب استخدام هذه الصيغة بدون استخدامها، بل باستخدام صيغة أقل عمومية أو من خلال تحويل التكامل باستخدام طريقة التغيير.

لنبدأ واحدة تلو الأخرى:

5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}

مع هذه الصيغة، في الواقع لا أعرف ما المشكلة، لأنها تنتج مباشرة من عكس صيغة المشتق:

{{\left( {{a}^{x}} \right)}^{\prime }}={{a}^{x}}\ln a

هنا، لا أظهر امتثالاً تاماً للأستاذ، بل أطلب توضيحاً عن كيفية حساب \int{{{3}^{x}}dx} بدون استخدام صيغة \int{{{a}^{x}}dx}.

إذا خطرت لأحدكم فكرة مثيرة، أرجو أن يشاركها مع الناس في التعليقات تحت المنشور.

9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}

حسناً، نعود إلى اللعبة.

هذه الصيغة لا تنتج مباشرة من عكس أي صيغة للمشتق.

إذا اتفقنا أننا لا نعرفها، يمكننا حساب التكامل \int{tgxdx} باستخدام التغيير:

10.\quad \int{ctgxdx=\ln \left| \sin x \right|}+C

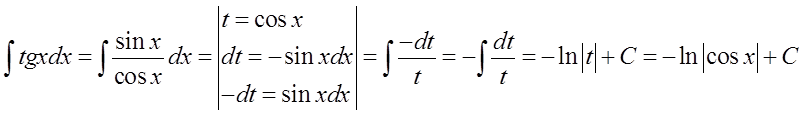
هنا بنفس الطريقة كما في السابق:

13.\quad \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}

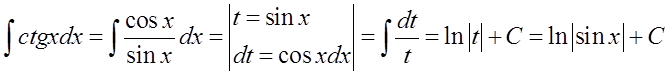
هذه الصيغة هي الشكل العام لصيغة:

\int{\frac{dx}{{{x}^{2}}+1}=arctgx+C} أو: \int{\frac{dx}{1+{{x}^{2}}}=arctgx+C}

يقصد الأستاذ هنا أن نستخدم الصيغة: \int{\frac{dx}{{{x}^{2}}+1}=arctgx+C}(التي تنتج من عكس بسيط لصيغة المشتق)، ولا نستخدم الصيغة: \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}(التي هي صيغة في شكلها “المعالج”).

نقوم بذلك على النحو التالي (بواسطة التحويل والتغيير):

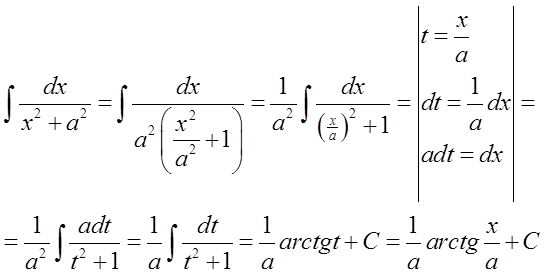
في مثال محدد، يمكن أن يبدو الأمر هكذا:

14.\quad \int{\frac{dx}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{2a}\ln \left| \frac{x-a}{x+a} \right|+C}

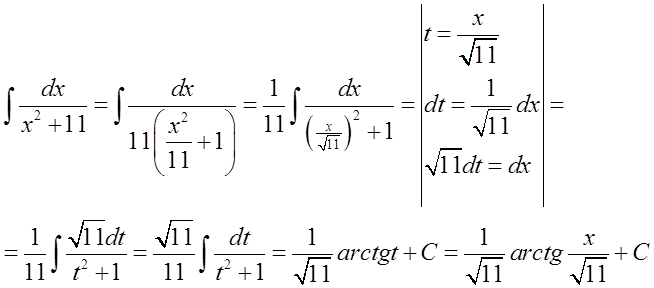
هذه الصيغة تختلف عن السابقة، ليس المقصود هنا استخدام صيغة يكون فيها ‘a’ بدلاً من ‘1’ (لا توجد مثل هذه الصيغة). البديل عن استخدام هذه الصيغة هو القيام بتحليل إلى كسور بسيطة كما في التكاملات الجبرية (شرحت كيفية القيام بذلك في الدرس 5 من دورة التكاملات غير المحددة).

في الواقع، \frac{1}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{\left( x-a \right)\left( x+a \right)}ومن ثم يمكن تحليلها إلى كسور بسيطة. على سبيل المثال:

\frac{1}{{{x}^{2}}-9}=\frac{1}{\left( x-3 \right)\left( x+3 \right)} \frac{1}{\left( x-3 \right)\left( x+3 \right)}=\frac{A}{x-3}+\frac{B}{x+3}

ثم نضرب في \left( x-3 \right)\left( x+3 \right)، نحسب الثوابت A, B بمقارنة الحدود وكما شرحت في الدرس 5 من الدورة.

15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}

هنا مرة أخرى، الصيغة العامة: \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}يجب تحويلها إلى الصيغة الخاصة: \int{\frac{dx}{\sqrt{1-{{x}^{2}}}}=\arcsin x+C}.

نقوم بذلك بطريقة مشابهة للصيغة 13):

في مثال محدد، يمكن أن يبدو الأمر هكذا:

16.\quad \int{\frac{dx}{\sqrt{{{x}^{2}}+q}}=\ln \left| x+\sqrt{{{x}^{2}}+q} \right|+C}

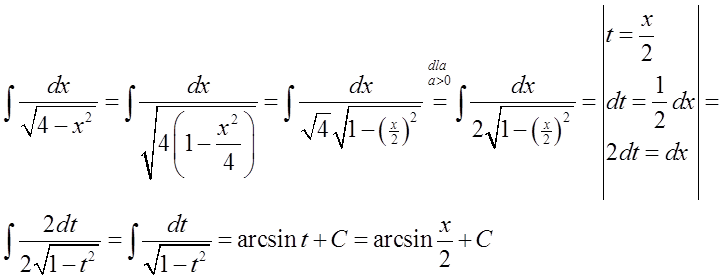
الموضوع أكثر تعقيداً، يتطلب استخدام ما يسمى “التغييرات الزائديّة” (مثل الزاوية الزائديّة). سأترك هذا الموضوع في هذا المنشور، وسأكتب عنه قريباً بالتأكيد.

هذه هي الصيغ التي سأل عنها المستخدم، وسأضيف من جانبي أن الصيغ المضافة إلى قائمة الصيغ الأساسية من قبلي:

\int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C \int{\sin axdx}=-\frac{1}{a}\cos ax+C \int{\cos axdx}=\frac{1}{a}\sin ax+C

يمكن استخلاصها بسهولة من خلال التغيير البسيط: t=ax

لذا عندنا على سبيل المثال التكامل: \int{{{e}^{-x}}dx}وعدم القدرة على استخدام (بسبب تفضيلات الأستاذ) الصيغة \int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C، نستخدم التغيير t=-xونكمل الحساب بهدوء.