W minionym roku szkolnym 2024/25 oraz obecnym roku szkolnym 2025/26, podobnie jak w poprzednich latach, podstawa programowa obowiązująca na egzaminie maturalnym została pomniejszona o pewne treści. Ministerstwo Edukacji i Nauki wyszło na przeciw uczniom i dnia 28 czerwca 2024 r. wydało rozporządzenie dokonujące pewnych zmian w egzaminie oraz w wymogach programowych do tego egzaminu obowiązującego po reformie edukacji, a więc dla uczniów, którzy ukończyli 8-letnią szkołę podstawową oraz 4- lub 5-letnią szkołę średnią. Treść rozporządzenia można znaleźć TUTAJ.
W przypadku egzaminu maturalnego 2026 w poniższych linkach znajdziecie Informatory o egzaminie maturalnym z matematyki, w których znajdują się liczne przykładowe zadania maturalne (wraz z odpowiedziami).
Informator o egzaminie maturalnym z matematyki, poziom podstawowy.
Informator o egzaminie maturalnym z matematyki, poziom rozszerzony.
Poniżej prezentujemy podsumowanie najważniejszych zmian na poziomie podstawowym oraz poziomie rozszerzonym, a także pełną podstawę programową (obowiązującą ogólnie po reformie) z zaznaczonymi treściami, które zostały usunięte dla uczniów zdających egzamin maturalny po reformie w latach szkolnych 2024/25 oraz 2025/26.
NAJWAŻNIEJSZE ZMIANY na poziomie podstawowym (NOWA FORMUŁA 2023):
![]()
![]() Za rozwiązanie zadań można uzyskać maksymalnie 50 punktów, w tym: 25 pkt – zadania zamknięte; 25 pkt – zadania otwarte.
Za rozwiązanie zadań można uzyskać maksymalnie 50 punktów, w tym: 25 pkt – zadania zamknięte; 25 pkt – zadania otwarte.
![]()
![]() Liczba zadań zamkniętych: 20-25
Liczba zadań zamkniętych: 20-25
![]()
![]() Liczba zadań otwartych: 7-14
Liczba zadań otwartych: 7-14
![]()
![]() Brak pewnych treści w podstawie programowej, w tym:
Brak pewnych treści w podstawie programowej, w tym:
![]() brak nierówności z wartością bezwzględną;
brak nierówności z wartością bezwzględną;
![]() brak wzorów skróconego mnożenia z potęgą 3 oraz potęgą n;
brak wzorów skróconego mnożenia z potęgą 3 oraz potęgą n;
![]() brak rozkładu wielomianów na czynniki metodą wyłączania wspólnego czynnika przed nawias oraz metodą grupowania wyrazów;
brak rozkładu wielomianów na czynniki metodą wyłączania wspólnego czynnika przed nawias oraz metodą grupowania wyrazów;
![]() brak znajdowania pierwiastków całkowitych wielomianu o współczynnikach całkowitych;
brak znajdowania pierwiastków całkowitych wielomianu o współczynnikach całkowitych;
![]() brak dzielenia wielomianu jednej zmiennej
brak dzielenia wielomianu jednej zmiennej ![]() przez dwumian postaci
przez dwumian postaci ![]() ;
;
![]() brak dodawania i odejmowania wyrażeń wymiernych;
brak dodawania i odejmowania wyrażeń wymiernych;
![]() brak równań dwukwadratowych;
brak równań dwukwadratowych;
![]() brak równań wymiernych postaci
brak równań wymiernych postaci 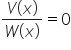 , gdzie wielomiany te są zapisane w postaci iloczynowej;
, gdzie wielomiany te są zapisane w postaci iloczynowej;
![]() brak układów równań postaci
brak układów równań postaci 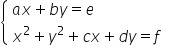 lub
lub 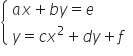 ;
;
![]() brak przekształcenia wykresów funkcji typu
brak przekształcenia wykresów funkcji typu ![]() lub
lub ![]() ;
;
![]() brak znajdowania wartości funkcji trygonometrycznej dla zadanego kąta za pomocą tablic lub kalkulatora oraz znajdowania kąta, dla którego dana wartość jest osiągana za pomocą tablic lub kalkulatora;
brak znajdowania wartości funkcji trygonometrycznej dla zadanego kąta za pomocą tablic lub kalkulatora oraz znajdowania kąta, dla którego dana wartość jest osiągana za pomocą tablic lub kalkulatora;
![]() brak twierdzenia odwrotnego do twierdzenia Talesa, o dwusiecznej kąta oraz o kącie między styczną a cięciwą;
brak twierdzenia odwrotnego do twierdzenia Talesa, o dwusiecznej kąta oraz o kącie między styczną a cięciwą;
![]() brak równania prostej prostopadłej do zadanej prostej i prostej stycznej do zadanego okręgu;
brak równania prostej prostopadłej do zadanej prostej i prostej stycznej do zadanego okręgu;
![]() brak odległości punktu od prostej;
brak odległości punktu od prostej;
![]() brak znajdowania punktów wspólnych prostej i okręgu oraz prostej i paraboli będącej wykresem funkcji kwadratowej;
brak znajdowania punktów wspólnych prostej i okręgu oraz prostej i paraboli będącej wykresem funkcji kwadratowej;
![]() brak określania, jaką figurą jest dany przekrój prostopadłościanu płaszczyzną;
brak określania, jaką figurą jest dany przekrój prostopadłościanu płaszczyzną;
![]() brak posługiwania się skalą centylową;
brak posługiwania się skalą centylową;
![]() brak obliczania odchylenia standardowego;
brak obliczania odchylenia standardowego;
![]() brak wyznaczania wartości oczekiwanej.
brak wyznaczania wartości oczekiwanej.
NAJWAŻNIEJSZE ZMIANY na poziomie rozszerzonym (NOWA FORMUŁA 2023):
![]()
![]() Obowiązek przystąpienia do egzaminu z jednego przedmiotu na poziomie rozszerzonym; bez progu zaliczenia. Obowiązek uzyskania co najmniej 30% punktów z jednego z wybranych przedmiotów dodatkowych – od 2028 r.
Obowiązek przystąpienia do egzaminu z jednego przedmiotu na poziomie rozszerzonym; bez progu zaliczenia. Obowiązek uzyskania co najmniej 30% punktów z jednego z wybranych przedmiotów dodatkowych – od 2028 r.
![]()
![]() Za rozwiązanie zadań można uzyskać maksymalnie 50 punktów. Liczba zadań otwartych: 10-14
Za rozwiązanie zadań można uzyskać maksymalnie 50 punktów. Liczba zadań otwartych: 10-14
![]()
![]() Przeprowadzany na podstawie wymagań egzaminacyjnych, zawierających ograniczony zakres wymagań podstawy programowej.
Przeprowadzany na podstawie wymagań egzaminacyjnych, zawierających ograniczony zakres wymagań podstawy programowej.
![]()
![]() Część treści zostało przeniesionych z poziomu podstawowego na poziom rozszerzony:
Część treści zostało przeniesionych z poziomu podstawowego na poziom rozszerzony:
![]() dzielenie wielomianu jednej zmiennej
dzielenie wielomianu jednej zmiennej ![]() przez dwumian postaci
przez dwumian postaci ![]() ;
;
![]() wzory skróconego mnożenia z potęgą 3;
wzory skróconego mnożenia z potęgą 3;
![]() rozkład wielomianów na czynniki metodą wyłączania wspólnego czynnika przed nawias oraz metodą grupowania wyrazów;
rozkład wielomianów na czynniki metodą wyłączania wspólnego czynnika przed nawias oraz metodą grupowania wyrazów;
![]() dodawanie i odejmowanie wyrażeń wymiernych;
dodawanie i odejmowanie wyrażeń wymiernych;
![]() równania dwukwadratowe;
równania dwukwadratowe;
![]() równania wymierne postaci
równania wymierne postaci 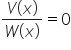 , gdzie wielomiany są zapisane w postaci iloczynowej;
, gdzie wielomiany są zapisane w postaci iloczynowej;
![]() rozwiązywanie metodą podstawiania układy równań, z których jedno jest liniowe, a drugie kwadratowe, postaci
rozwiązywanie metodą podstawiania układy równań, z których jedno jest liniowe, a drugie kwadratowe, postaci 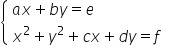 lub
lub 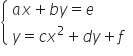 ;
;
![]() przekształcenia wykresów funkcji typu
przekształcenia wykresów funkcji typu ![]() lub
lub ![]() ;
;
![]() twierdzenie sinusów wraz z jego zastosowaniem;
twierdzenie sinusów wraz z jego zastosowaniem;
![]() obliczanie kątów trójkąta i długości jego boków przy odpowiednich danych (m.in. z wykorzystaniem twierdzenia sinusów lub cosinusów)
obliczanie kątów trójkąta i długości jego boków przy odpowiednich danych (m.in. z wykorzystaniem twierdzenia sinusów lub cosinusów)
![]() twierdzenie odwrotne do twierdzenia Talesa;
twierdzenie odwrotne do twierdzenia Talesa;
![]() wyznaczanie równania prostej prostopadłej do zadanej prostej i prostej stycznej do zadanego okręgu;
wyznaczanie równania prostej prostopadłej do zadanej prostej i prostej stycznej do zadanego okręgu;
![]() znajdowanie punktów wspólnych prostej i okręgu.
znajdowanie punktów wspólnych prostej i okręgu.
![]()
![]() Część treści zostało usuniętych z poziomu rozszerzonego:
Część treści zostało usuniętych z poziomu rozszerzonego:
![]() brak znajdywania pierwiastków wymiernych wielomianu o współczynnikach całkowitych;
brak znajdywania pierwiastków wymiernych wielomianu o współczynnikach całkowitych;
![]() brak przekształcenia wykresów funkcji typu:
brak przekształcenia wykresów funkcji typu: ![]() ;
;
![]() brak nierówności trygonometrycznych;
brak nierówności trygonometrycznych;
![]() brak własności Darboux do znajdowania przybliżonej wartości miejsca zerowego.
brak własności Darboux do znajdowania przybliżonej wartości miejsca zerowego.
Na czerwono wyszczególniono treści, które NIE obowiązują na danym poziomie na maturze w roku 2025 i roku 2026.
Na zielono wyszczególniono treści, które zostały PRZESUNIĘTE z poziomu podstawowego do poziomu rozszerzonego na maturze w roku 2025 i roku 2026.
Treści nauczania – wymagania szczegółowe
I. Liczby rzeczywiste.
Zakres podstawowy. Uczeń:
1. wykonuje działania (dodawanie, odejmowanie, mnożenie, dzielenie, potęgowanie, pierwiastkowanie, logarytmowanie) w zbiorze liczb rzeczywistych;
2. przeprowadza proste dowody dotyczące podzielności liczb całkowitych i reszt z dzielenia nie trudniejsze niż:
a) dowód podzielności przez 24 iloczynu czterech kolejnych liczb naturalnych,
b) dowód własności: jeśli liczba przy dzieleniu przez 4 daje resztę 3, to nie jest kwadratem liczby całkowitej;
3. stosuje własności pierwiastków dowolnego stopnia, w tym pierwiastków stopnia nieparzystego z liczb ujemnych;
4. stosuje związek pierwiastkowania z potęgowaniem oraz prawa działań na potęgach i pierwiastkach;
5. stosuje własności monotoniczności potęgowania, w szczególności własności: jeśli ![]() oraz
oraz ![]() , to
, to ![]() , zaś gdy
, zaś gdy ![]() i
i ![]() , to
, to ![]() ;
;
6. posługuje się pojęciem przedziału liczbowego, zaznacza przedziały na osi liczbowej;
7. stosuje interpretację geometryczną i algebraiczną wartości bezwzględnej, rozwiązuje równania i nierówności typu: ![]() ,
, ![]() ,
, ![]() ;
;
8. wykorzystuje własności potęgowania i pierwiastkowania w sytuacjach praktycznych, w tym do obliczania procentów składanych z kapitalizacją roczną, zysków z lokat i kosztów kredytów;
9. stosuje związek logarytmowania z potęgowaniem, posługuje się wzorami na logarytm iloczynu, logarytm ilorazu i logarytm potęgi.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. stosuje wzór na zamianę podstawy logarytmu;
II. Wyrażenia algebraiczne.
Zakres podstawowy. Uczeń:
1. stosuje wzory skróconego mnożenia na: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
2. dodaje, odejmuje i mnoży wielomiany jednej i wielu zmiennych;
3. wyłącza poza nawias jednomian z sumy algebraicznej;
4. rozkłada wielomiany na czynniki metodą wyłączania wspólnego czynnika przed nawias oraz metodą grupowania wyrazów, w przypadkach nie trudniejszych niż rozkład wielomianu ![]() ;
;
5. znajduje pierwiastki całkowite wielomianu o współczynnikach całkowitych;
6. dzieli wielomian jednej zmiennej ![]() przez dwumian postaci
przez dwumian postaci ![]() ;
;
7. mnoży i dzieli wyrażenia wymierne;
8. dodaje i odejmuje wyrażenia wymierne, w przypadkach nie trudniejszych niż: ![]() ,
, ![]() ,
, ![]() .
.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. znajduje pierwiastki całkowite i wymierne wielomianu o współczynnikach całkowitych;
2. dzieli wielomian jednej zmiennej ![]() przez dwumian postaci
przez dwumian postaci ![]() ; (przeniesione z poziomu podstawowego)
; (przeniesione z poziomu podstawowego)
3. rozkłada wielomiany na czynniki metodą wyłączania wspólnego czynnika przed nawias oraz metodą grupowania wyrazów, w przypadkach nie trudniejszych niż rozkład wielomianu ![]() ; (przeniesione z poziomu podstawowego)
; (przeniesione z poziomu podstawowego)
4. stosuje podstawowe własności trójkąta Pascala oraz następujące własności współczynnika dwumianowego (symbolu Newtona): 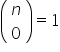 ,
, 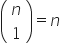 ,
, 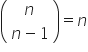 ,
, 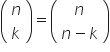 ,
, 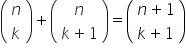 ;
;
5. korzysta ze wzorów na: ![]() ,
, ![]() ,
, ![]() (przeniesione z poziomu podstawowego) ,
(przeniesione z poziomu podstawowego) , ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
6. dodaje i odejmuje wyrażenia wymierne, w przypadkach nie trudniejszych niż: ![]() ,
, ![]() ,
, ![]() . (przeniesione z poziomu podstawowego)
. (przeniesione z poziomu podstawowego)
III. Równania i nierówności.
Zakres podstawowy. Uczeń:
1. przekształca równania i nierówności w sposób równoważny, w tym np. przekształca równoważnie równanie ![]() ;
;
2. interpretuje równania i nierówności sprzeczne oraz tożsamościowe;
3. rozwiązuje nierówności liniowe z jedną niewiadomą;
4. rozwiązuje równania i nierówności kwadratowe;
5. rozwiązuje równania wielomianowe, które dają się doprowadzić do równania kwadratowego, w szczególności równania dwukwadratowe;
6. rozwiązuje równania wielomianowe postaci ![]() dla wielomianów doprowadzonych do postaci iloczynowej lub takich, które dają się doprowadzić do postaci iloczynowej metodą wyłączania wspólnego czynnika przed nawias lub metodą grupowania;
dla wielomianów doprowadzonych do postaci iloczynowej lub takich, które dają się doprowadzić do postaci iloczynowej metodą wyłączania wspólnego czynnika przed nawias lub metodą grupowania;
7. rozwiązuje równania wymierne postaci 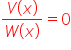 , gdzie wielomiany
, gdzie wielomiany ![]() i
i ![]() są zapisane w postaci iloczynowej.
są zapisane w postaci iloczynowej.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. rozwiązuje równania wielomianowe postaci ![]() oraz nierówności wielomianowe typu:
oraz nierówności wielomianowe typu: ![]() ,
, ![]() ,
, ![]() ,
, ![]() dla wielomianów doprowadzonych do postaci iloczynowej lub takich, które dają się doprowadzić do postaci iloczynowej metodą wyłączania wspólnego czynnika przed nawias lub metodą grupowania;
dla wielomianów doprowadzonych do postaci iloczynowej lub takich, które dają się doprowadzić do postaci iloczynowej metodą wyłączania wspólnego czynnika przed nawias lub metodą grupowania;
2. rozwiązuje równania i nierówności wymierne, które dadzą się sprowadzić do równania lub nierówności liniowej lub kwadratowej, np. ![]() ;
;
3. stosuje wzory Viète’a dla równań kwadratowych;
4. rozwiązuje równania i nierówności z wartością bezwzględną, o stopniu trudności nie większym niż: ![]() ,
, ![]() ;
;
5. analizuje równania i nierówności liniowe z parametrami oraz równania i nierówności kwadratowe z parametrami, w szczególności: wyznacza liczbę rozwiązań w zależności od parametrów, podaje warunki, przy których rozwiązania mają określone znaki bądź należą do określonego przedziału, wyznacza rozwiązania w zależności od parametrów;
6. rozwiązuje równania wielomianowe, które dają się doprowadzić do równania kwadratowego, w szczególności równania dwukwadratowe; (przeniesione z poziomu podstawowego)
7. rozwiązuje równania wymierne postaci 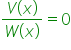 , gdzie wielomiany
, gdzie wielomiany ![]() i
i ![]() są zapisane postaci iloczynowej. (przeniesione z poziomu podstawowego)
są zapisane postaci iloczynowej. (przeniesione z poziomu podstawowego)
IV. Układy równań.
Zakres podstawowy. Uczeń:
1. rozwiązuje układy równań liniowych z dwiema niewiadomymi, podaje interpretację geometryczną układów oznaczonych, nieoznaczonych i sprzecznych;
2. stosuje układy równań do rozwiązywania zadań tekstowych;
3. rozwiązuje metodą podstawiania układy równań, z których jedno jest liniowe, a drugie kwadratowe, postaci 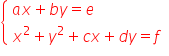 lub
lub 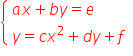 .
.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. rozwiązuje metodą podstawiania układy równań, z których jedno jest liniowe, a drugie kwadratowe, postaci 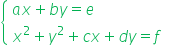 lub
lub 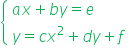 ; (przeniesione z poziomu podstawowego)
; (przeniesione z poziomu podstawowego)
2. rozwiązuje układy równań kwadratowych postaci 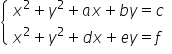 .
.
V. Funkcje.
Zakres podstawowy. Uczeń:
1. określa funkcje jako jednoznaczne przyporządkowanie za pomocą opisu słownego, tabeli, wykresu, wzoru (także różnymi wzorami na różnych przedziałach);
2. oblicza wartość funkcji zadanej wzorem algebraicznym;
3. odczytuje i interpretuje wartości funkcji określonych za pomocą tabel, wykresów, wzorów itp., również w sytuacjach wielokrotnego użycia tego samego źródła informacji lub kilku źródeł jednocześnie;
4. odczytuje z wykresu funkcji: dziedzinę, zbiór wartości, miejsca zerowe, przedziały monotoniczności, przedziały, w których funkcja przyjmuje wartości większe (nie mniejsze) lub mniejsze (nie większe) od danej liczby, największe i najmniejsze wartości funkcji (o ile istnieją) w danym przedziale domkniętym oraz argumenty, dla których wartości największe i najmniejsze są przez funkcję przyjmowane;
5. interpretuje współczynniki występujące we wzorze funkcji liniowej;
6. wyznacza wzór funkcji liniowej na podstawie informacji o jej wykresie lub o jej własnościach;
7. szkicuje wykres funkcji kwadratowej zadanej wzorem;
8. interpretuje współczynniki występujące we wzorze funkcji kwadratowej w postaci ogólnej, kanonicznej i iloczynowej (jeśli istnieje);
9. wyznacza wzór funkcji kwadratowej na podstawie informacji o tej funkcji lub o jej wykresie;
10. wyznacza największą i najmniejszą wartość funkcji kwadratowej w przedziale domkniętym;
11. wykorzystuje własności funkcji liniowej i kwadratowej do interpretacji zagadnień geometrycznych, fizycznych itp., także osadzonych w kontekście praktycznym;
12. na podstawie wykresu funkcji ![]() szkicuje wykresy funkcji
szkicuje wykresy funkcji ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
13. posługuje się funkcją ![]() , w tym jej wykresem, do opisu i interpretacji zagadnień związanych z wielkościami odwrotnie proporcjonalnymi, również w zastosowaniach praktycznych;
, w tym jej wykresem, do opisu i interpretacji zagadnień związanych z wielkościami odwrotnie proporcjonalnymi, również w zastosowaniach praktycznych;
14. posługuje się funkcjami wykładniczą i logarytmiczną, w tym ich wykresami, do opisu i interpretacji zagadnień związanych z zastosowaniami praktycznymi.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. na podstawie wykresu funkcji ![]() rysuje wykresy funkcji
rysuje wykresy funkcji ![]() ,
, ![]() , (przeniesione z poziomu podstawowego) ,
, (przeniesione z poziomu podstawowego) , ![]() ;
;
2. posługuje się złożeniami funkcji;
3. dowodzi monotoniczności funkcji zadanej wzorem, jak w przykładzie: wykaż, że funkcja ![]() jest monotoniczna w przedziale
jest monotoniczna w przedziale ![]() .
.
VI. Ciągi.
Zakres podstawowy. Uczeń:
1. oblicza wyrazy ciągu określonego wzorem ogólnym;
2. oblicza początkowe wyrazy ciągów określonych rekurencyjnie, jak w przykładach:
a) 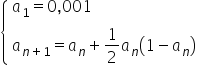 ,
,
b) 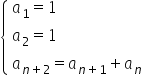 .
.
3. w prostych przypadkach bada, czy ciąg jest rosnący, czy malejący;
4. sprawdza, czy dany ciąg jest arytmetyczny lub geometryczny;
5. stosuje wzór na n-ty wyraz i na sumę n początkowych wyrazów ciągu arytmetycznego;
6. stosuje wzór na n-ty wyraz i na sumę n początkowych wyrazów ciągu geometrycznego;
7. wykorzystuje własności ciągów, w tym arytmetycznych i geometrycznych, do rozwiązywania zadań, również osadzonych w kontekście praktycznym.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. oblicza granice ciągów, korzystając z granic ciągów typu ![]() ,
, ![]() oraz twierdzeń o granicach sumy, różnicy, iloczynu i ilorazu ciągów zbieżnych, a także twierdzenia o trzech ciągach;
oraz twierdzeń o granicach sumy, różnicy, iloczynu i ilorazu ciągów zbieżnych, a także twierdzenia o trzech ciągach;
2. rozpoznaje zbieżne szeregi geometryczne i oblicza ich sumę.
VII. Trygonometria.
Zakres podstawowy. Uczeń:
1. wykorzystuje definicje funkcji: sinus, cosinus i tangens dla kątów od 0° do 180° , w szczególności wyznacza wartości funkcji trygonometrycznych dla kątów 30°, 45°, 60°;
2. znajduje przybliżone wartości funkcji trygonometrycznych, korzystając z tablic lub kalkulatora;
3. znajduje za pomocą tablic lub kalkulatora przybliżoną wartość kąta, jeśli dana jest wartość funkcji trygonometrycznej;
4. korzysta z wzorów ![]() ,
, ![]() ;
;
5. stosuje twierdzenie sinusów i twierdzenie cosinusów oraz wzór na pole trójkąta ![]() ;
;
6. oblicza kąty trójkąta prostokątnego i długości jego boków przy odpowiednich danych (rozwiązuje trójkąty prostokątne, w tym z wykorzystaniem funkcji trygonometrycznych).
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. stosuje miarę łukową, zamienia stopnie na radiany i odwrotnie;
2. posługuje się wykresami funkcji trygonometrycznych: sinus, cosinus, tangens;
3. wykorzystuje okresowość funkcji trygonometrycznych;
4. stosuje wzory redukcyjne dla funkcji trygonometrycznych;
5. korzysta z wzorów na sinus, cosinus i tangens sumy i różnicy kątów, a także na funkcje trygonometryczne kątów podwojonych;
6. rozwiązuje równania i nierówności trygonometryczne;
7. stosuje twierdzenie sinusów; (przeniesione z poziomu podstawowego)
8. oblicza kąty trójkąta i długości jego boków przy odpowiednich danych (m.in. z wykorzystaniem twierdzenia sinusów lub cosinusów). (przeniesione z poziomu podstawowego)
VIII. Planimetria.
Zakres podstawowy. Uczeń:
1. wyznacza promienie i średnice okręgów, długości cięciw okręgów oraz odcinków stycznych, w tym z wykorzystaniem twierdzenia Pitagorasa;
2. rozpoznaje trójkąty ostrokątne, prostokątne i rozwartokątne przy danych długościach boków (m.in. stosuje twierdzenie odwrotne do twierdzenia Pitagorasa i twierdzenie cosinusów); stosuje twierdzenie: w trójkącie naprzeciw większego kąta wewnętrznego leży dłuższy bok;
3. rozpoznaje wielokąty foremne i korzysta z ich podstawowych własności;
4. korzysta z własności kątów i przekątnych w prostokątach, równoległobokach, rombach i trapezach;
5. stosuje własności kątów wpisanych i środkowych;
6. stosuje wzory na pole wycinka koła i długość łuku okręgu;
7. stosuje twierdzenia: Talesa, odwrotne do twierdzenia Talesa, o dwusiecznej kąta oraz o kącie między styczną a cięciwą;
8. korzysta z cech podobieństwa trójkątów;
9. wykorzystuje zależności między obwodami oraz między polami figur podobnych;
10. wskazuje podstawowe punkty szczególne w trójkącie: środek okręgu wpisanego w trójkąt, środek okręgu opisanego na trójkącie, ortocentrum, środek ciężkości oraz korzysta z ich własności;
11. stosuje funkcje trygonometryczne do wyznaczania długości odcinków w figurach płaskich oraz obliczania pól figur;
12. przeprowadza dowody geometryczne.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. stosuje własności czworokątów wpisanych w okrąg i opisanych na okręgu.
2. stosuje twierdzenie odwrotne do twierdzenia Talesa; (przeniesione z poziomu podstawowego)
IX. Geometria analityczna na płaszczyźnie kartezjańskiej.
Zakres podstawowy. Uczeń:
1. rozpoznaje wzajemne położenie prostych na płaszczyźnie na podstawie ich równań, w tym znajduje wspólny punkt dwóch prostych, jeśli taki istnieje;
2. posługuje się równaniami prostych na płaszczyźnie, w postaci kierunkowej i ogólnej, w tym wyznacza równanie prostej o zadanych własnościach (takich jak na przykład przechodzenie przez dwa dane punkty, znany współczynnik kierunkowy, równoległość lub prostopadłość do innej prostej, styczność do okręgu);
3. oblicza odległość dwóch punktów w układzie współrzędnych;
4. posługuje się równaniem okręgu ![]() ;
;
5. oblicza odległość punktu od prostej;
6. znajduje punkty wspólne prostej i okręgu oraz prostej i paraboli będącej wykresem funkcji kwadratowej;
7. wyznacza obrazy okręgów i wielokątów w symetriach osiowych względem osi układu współrzędnych, symetrii środkowej (o środku w początku układu współrzędnych).
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. znajduje punkty wspólne prostej i okręgu; (przeniesione z poziomu podstawowego)
2. znajduje punkty wspólne dwóch okręgów;
3. zna pojęcie wektora i oblicza jego współrzędne oraz długość, dodaje wektory i mnoży wektor przez liczbę, oba te działania wykonuje zarówno analitycznie, jak i geometrycznie.
5. wyznacza równanie prostej prostopadłej do zadanej prostej i prostej stycznej do zadanego okręgu. (przeniesione z poziomu podstawowego)
X. Stereometria.
Zakres podstawowy. Uczeń:
1. rozpoznaje wzajemne położenie prostych w przestrzeni, w szczególności proste prostopadłe nieprzecinające się;
2. posługuje się pojęciem kąta między prostą a płaszczyzną oraz pojęciem kąta dwuściennego między półpłaszczyznami;
3. rozpoznaje w graniastosłupach i ostrosłupach kąty między odcinkami (np. krawędziami, krawędziami i przekątnymi) oraz kąty między ścianami, oblicza miary tych kątów;
4. rozpoznaje w walcach i w stożkach kąt między odcinkami oraz kąt między odcinkami i płaszczyznami (np. kąt rozwarcia stożka, kąt między tworzącą a podstawą), oblicza miary tych kątów;
5. określa, jaką figurą jest dany przekrój prostopadłościanu płaszczyzną;
6. oblicza objętości i pola powierzchni graniastosłupów, ostrosłupów, walca, stożka i kuli, również z wykorzystaniem trygonometrii i poznanych twierdzeń;
7. wykorzystuje zależność między objętościami brył podobnych.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. zna i stosuje twierdzenie o prostej prostopadłej do płaszczyzny i o trzech prostopadłych;
2. wyznacza przekroje sześcianu i ostrosłupów prawidłowych oraz oblicza ich pola, także z wykorzystaniem trygonometrii.
XI. Kombinatoryka.
Zakres podstawowy. Uczeń:
1. zlicza obiekty w prostych sytuacjach kombinatorycznych;
2. zlicza obiekty, stosując reguły mnożenia i dodawania (także łącznie) dla dowolnej liczby czynności w sytuacjach nie trudniejszych niż:
a) obliczenie, ile jest czterocyfrowych nieparzystych liczb całkowitych dodatnich takich, że w ich zapisie dziesiętnym występuje dokładnie jedna cyfra 1 i dokładnie jedna cyfra 2,
b) obliczenie, ile jest czterocyfrowych parzystych liczb całkowitych dodatnich takich, że w ich zapisie dziesiętnym występuje dokładnie jedna cyfra 0 i dokładnie jedna cyfra 1.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. oblicza liczbę możliwych sytuacji, spełniających określone kryteria, z wykorzystaniem reguły mnożenia i dodawania (także łącznie) oraz wzorów na liczbę: permutacji, kombinacji i wariacji, również w przypadkach wymagających rozważenia złożonego modelu zliczania elementów;
2. stosuje współczynnik dwumianowy (symbol Newtona) i jego własności przy rozwiązywaniu problemów kombinatorycznych.
XII. Rachunek prawdopodobieństwa i statystyka.
Zakres podstawowy. Uczeń:
1. oblicza prawdopodobieństwo w modelu klasycznym;
2. stosuje skalę centylową;
3. oblicza średnią arytmetyczną i średnią ważoną, znajduje medianę i dominantę;
4. oblicza odchylenie standardowe zestawu danych (także w przypadku danych odpowiednio pogrupowanych), interpretuje ten parametr dla danych empirycznych;
5. oblicza wartość oczekiwaną, np. przy ustalaniu wysokości wygranej w prostych grach losowych i loteriach.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. oblicza prawdopodobieństwo warunkowe i stosuje wzór Bayesa, stosuje twierdzenie o prawdopodobieństwie całkowitym;
2. stosuje schemat Bernoulliego.
XIII. Optymalizacja i rachunek różniczkowy.
Zakres podstawowy. Uczeń:
1. rozwiązuje zadania optymalizacyjne w sytuacjach dających się opisać funkcją kwadratową.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. oblicza granice funkcji (w tym jednostronne);
2. stosuje własność Darboux do uzasadniania istnienia miejsca zerowego funkcji i znajdowania przybliżonej wartości miejsca zerowego;
3. stosuje definicję pochodnej funkcji, podaje interpretację geometryczną i fizyczną pochodnej;
4. oblicza pochodną funkcji potęgowej o wykładniku rzeczywistym oraz oblicza pochodną, korzystając z twierdzeń o pochodnej sumy, różnicy, iloczynu, ilorazu i funkcji złożonej;
5. stosuje pochodną do badania monotoniczności funkcji;
6. rozwiązuje zadania optymalizacyjne z zastosowaniem pochodnej.
Źródło:
https://isap.sejm.gov.pl/isap.nsf/download.xsp/WDU20240001019/O/D20241019.pdf


