Słysząc „zmienne ekonomiczne”, z reguły mamy na myśli zmienne, które można łatwo wyrazić liczbowo, policzyć. Typu: ceny, wydatki, dochód, temperatura powietrza, ilość samochodów, liczba lekarzy etc.
Są to tzw. zmienne ilościowe.
Ale co jeśli w modelu potrzebujemy ująć zmienne o charakterze nieliczbowym, tzn. wyrażane bardziej poprzez słowa niż przez liczby?
Chodzi mi o: tak – nie, kobieta – mężczyzna, żonaty – kawaler, pracuje – nie pracuje, wyznawana religia, wykształcenie (wyższe – średnie – podstawowe), pochodzenie (ze wsi – z miasta małego – z miasta dużego), itp. Mogą mieć z reguły dwa lub więcej wariantów odpowiedzi. One również mają wpływ na wartość wyjaśnianej cechy.
Jest to drugi typ zmiennych w modelu – zmienne jakościowe.
Przykład 1
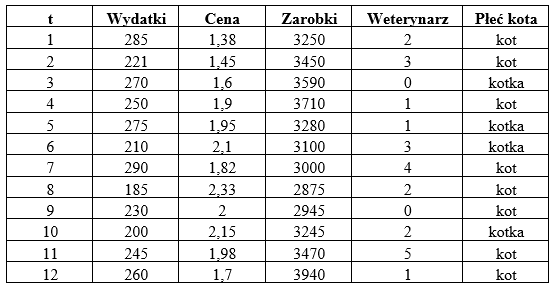
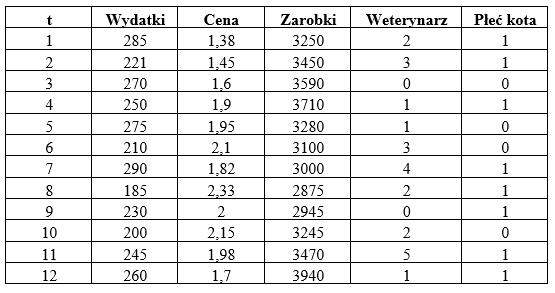
Pani Grażynka przez cały rok zbierała dane dotyczące wydatków na karmę (w zł) dla jej dwóch kotów – Kici i Pirata. Chciałaby przeprowadzić analizę tych kosztów w zależności od kilku czynników, jej zdaniem najbardziej na to wpływających. Jako zmienne objaśniające wybrała: średnią cenę za 1 kilogram karmy, wysokość miesięcznych zarobków jej męża Janusza (w zł), ilość wizyt u weterynarza w miesiącu oraz kto jadł częściej z ich ulubionej miseczki – kot czy kotka.
Model ekonometryczny liniowy tłumaczący wybrane zależności jest następujący:
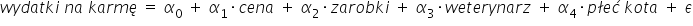 W poniższej tabeli znajdziesz wyniki zebrane przez Panią Grażynkę:
W poniższej tabeli znajdziesz wyniki zebrane przez Panią Grażynkę:
Powiedzmy, że wszystkie te zmienne są istotne, wchodzą do modelu. Potrzebuję teraz oszacować parametry strukturalne, czyli alfy. Ale, ale, przecież do obliczeń nie wykorzystam słowa „kot” albo „kotka” – liczenie to nie literki. My potrzebujemy konkretnych cyfr 🙂 Co więc zrobić ze zmienną „płeć kota”, skoro wyrażona jest ona tylko poprzez słowa? Odrzucić?
Jak większości problemów, zaradzono i temu. Wymyślono, by wartości zmiennych jakościowych, które mają dwa warianty odpowiedzi, zastąpić cyframi: „1” oraz „0”. Stąd dana cecha przyjmuje wartości:
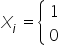
gdzie:
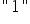 – stawiamy, gdy zdarzenie wystąpi (obiekt ma daną cechę);
– stawiamy, gdy zdarzenie wystąpi (obiekt ma daną cechę);
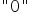 – w przypadku przeciwnym, czyli gdy zdarzenie nie wystąpi (obiekt nie ma wybranej cechy)
– w przypadku przeciwnym, czyli gdy zdarzenie nie wystąpi (obiekt nie ma wybranej cechy)
Wystarczy teraz przypisać odpowiednią cyfrę do danego wariantu zmiennej. Pani Grażynka uznała, że Pirat będzie miał numer „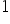 „, zaś Kicia numer „
„, zaś Kicia numer „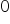 „. Oczywiście mogła wziąć cyferki odwrotnie, żaden problem, zwłaszcza jeśli chodzi o rozróżnianie płci. Kotce mogła być przypisana cyfra jeden, a kot byłby zerem.
„. Oczywiście mogła wziąć cyferki odwrotnie, żaden problem, zwłaszcza jeśli chodzi o rozróżnianie płci. Kotce mogła być przypisana cyfra jeden, a kot byłby zerem.
Mając już same liczby (takie jak podane w tabelce), na spokojnie możemy wykonać wszystkie obliczenia. Później wyniki odpowiednio zinterpretujemy. Tutaj będziesz musiał zwrócić uwagę na pewien aspekt – ale o tym za chwilę.
Tabela do obliczeń wygląda następująco:
Model oszacuję za pomocą Klasycznej Metody Najmniejszych Kwadratów stosowanej do liniowych modeli jednorównaniowych. Sposób w jaki estymuje się parametry strukturalne dokładnie pokazałam w moim Kursie. Oto wynik:
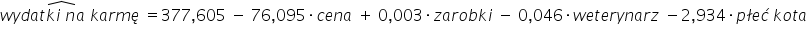
Jak widać, sama metoda estymacji, mając zmienną złożona z samych zer i jedynek, nie ulega zmianie. Jak jednak zinterpretować współczynnik stojący przy zmiennej „płeć kota”?
Interpretacja parametrów przy cenie, zarobkach czy ilości wizyt u weterynarza jest typowa.
Wzrost zmiennej objaśniającej o 1 jednostkę pociąga za sobą zmianę (wzrost lub spadek) zmiennej objaśnianej, w tym przykładzie wydatków na karmę, o wartość oszacowanego parametru 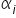 , oczywiście przy niezmienionych wartościach pozostałych zmiennych (ceteris paribus). Jednakże nie możesz tak samo zinterpretować zmiennej płeć kota. To raczej bez sensu powiedzieć, że „wzrost płci, znaczy zmiana z kotki na kota (?) (inaczej przejście z cechy oznaczonej
, oczywiście przy niezmienionych wartościach pozostałych zmiennych (ceteris paribus). Jednakże nie możesz tak samo zinterpretować zmiennej płeć kota. To raczej bez sensu powiedzieć, że „wzrost płci, znaczy zmiana z kotki na kota (?) (inaczej przejście z cechy oznaczonej 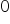 na cechę z przypisaną
na cechę z przypisaną 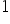 ) powoduje spadek wydatków na karmę o około 2,93 zł”. Dziwnie brzmi, prawda? 🙂
) powoduje spadek wydatków na karmę o około 2,93 zł”. Dziwnie brzmi, prawda? 🙂
Zatem, gdybyśmy chcieli zinterpretować parametr stojący przy zmiennej jakościowej, wyrażonej poprzez zero-jedynki, jak mamy to zrobić?
Przypatrz się uważnie, czemu jest przypisana wartość 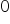 oraz
oraz 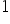 . W przykładzie mamy że
. W przykładzie mamy że 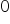 – kotka Kicia jadła częściej z ich ulubionej miseczki,
– kotka Kicia jadła częściej z ich ulubionej miseczki, 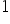 – kot Pirat jadł częściej z ich ulubionej miseczki. Zmienną objaśnianą Y jest wielkość wydatków na karmę dla kotów.
– kot Pirat jadł częściej z ich ulubionej miseczki. Zmienną objaśnianą Y jest wielkość wydatków na karmę dla kotów.
Interpretacja parametru 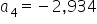 : Wielkość wydatków na karmę w przypadku, gdy z ulubionej miseczki jadł kot była mniejsza o około 2,93 zł w porównaniu gdy częściej z miseczki jadła kotka, przy takich samych wartościach pozostałych zmiennych.
: Wielkość wydatków na karmę w przypadku, gdy z ulubionej miseczki jadł kot była mniejsza o około 2,93 zł w porównaniu gdy częściej z miseczki jadła kotka, przy takich samych wartościach pozostałych zmiennych.
Popatrz, nie jest to trudne. Można napisać taki ogólny schemat, jak się interpretuje zmienne zero-jedynkowe:
Wielkość ..(zmienna objaśniana Y).. dla/w przypadku ..(cecha z przypisaną jedynką)..różni się przeciętnie mniej więcej o (i tu ocena parametru – pamiętaj, uwzględnij znak! „jest większa/mniejsza o około”) w porównaniu z ..(cecha z przypisanym zerem).. przy takich samych wartościach pozostałych zmiennych (napisać ewentualnie jakich).
Inny przykład by poćwiczyć interpretację (bo pamiętaj, liczenie liczeniem, ale wnioski jakie z tego wyciągniesz – to się najbardziej liczy w ekonometrii!).
Przykład 2
Badamy np. osobiste miesięczne wydatki na jedzenie (w zł). Wśród zmiennych objaśniających jest zmienna przyjmująca wartości: zamężna/żonaty – 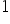 oraz panna/kawaler –
oraz panna/kawaler – 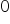 . Zatem w tabeli danych będziesz miał kolumnę złożoną z samych zer i jedynek, to już jest jasne. Po wykonaniu obliczeń otrzymano, że oszacowany parametr przy zmiennej „stan cywilny” wynosi
. Zatem w tabeli danych będziesz miał kolumnę złożoną z samych zer i jedynek, to już jest jasne. Po wykonaniu obliczeń otrzymano, że oszacowany parametr przy zmiennej „stan cywilny” wynosi 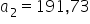 . Jego interpretacja leci tak:
. Jego interpretacja leci tak:
Wielkość wydatków na jedzenie osób zamężnych/żonatych jest większa o około 191,73 zł w porównaniu z osobami niezamężnymi/nieżonatymi przy takich samych wartościach pozostałych zmiennych (ceteris paribus). Inaczej byś powiedział, że osoby zamężne/żonate wydają miesięcznie więcej na jedzenie o około 191,73 zł od panien/kawalerów.
W sumie jedzonko na wikcie małżeńskim, gdy mąż lub żona gotuje, jest z reguły inne niż te za czasów kawalerskich 🙂
Widzisz jak działa ten schemat? Mam nadzieję, że jeśli teraz trafi Ci się model ze zmiennymi jakościowymi, to poradzisz również i z interpretacją takich zmiennych. Powodzenia 🙂
KONIEC