Całki Oznaczone Wykład 1
Temat: Całki Oznaczone – definicja
Streszczenie
W pierwszej części wykładu pokażę, czym jest całka oznaczona (w sensie Riemmana) i jak powstaje odpowiadający jej szereg. W drugiej wprowadzę ścisłą, matematyczną definicję.
Część I – całka oznaczona jako pewien szereg (suma)
Jak to często w matematyce bywa, całki oznaczone nie powstały sobie ot tak, „z niczego”. Całki oznaczone rozwiązują pewien – zupełnie prosty do zrozumienia – problem. Czyli najpierw był PROBLEM, a później pojawiły się całki oznaczone. Na czym polegał problem?
Problem dokładnego obliczenia pola
Zastanówmy się nad kwestią obliczania pola jakiegoś obszaru. Znamy wzory na pola: koła, kwadratu, prostokąta, równoległoboku, trapezu, rombu itd. Jest fajnie.
Co jednak jeśli obszar (np. kawałek lasu), który rozmiar chcemy policzyć nie jest takim równym: kołem, kwadratem, prostokątem, równoległobokiem, trapezem, rombem itd.? Mamy problem.
Sposób na obliczenie pola „nietypowego” obszaru
Na innym wykładzie (poświęconym całkom nieoznaczonym) przedstawiłem już pewien sposób na ugryzienie tej sprawy:
Całka nieoznaczona a obliczenia pola obszaru
Na tym wykładzie spróbujemy jednak z innej strony.
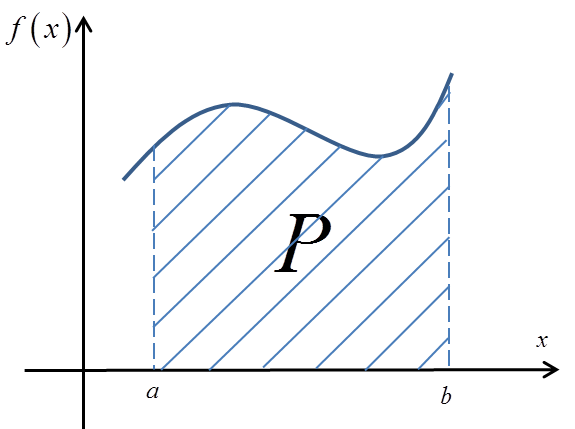
Narysujmy sobie obszar „nietypowy” i wprowadźmy układ współrzędnych:
Obszar, który narysowałem można nazwać 'trapezem krzywoliniowym” (bo jedna z podstaw jest krzywą). Jak się zastanowić, to właściwie każdego „kleksa”, czy obszar nieregularny da się podzielić na trapezy krzywoliniowe.
Zakładamy, że funkcję ![]() już znamy, czyli że jest ona DANA.
już znamy, czyli że jest ona DANA.
Jeśli tak, to dosyć łatwo policzyć możemy pola tych dwóch prostokątów:
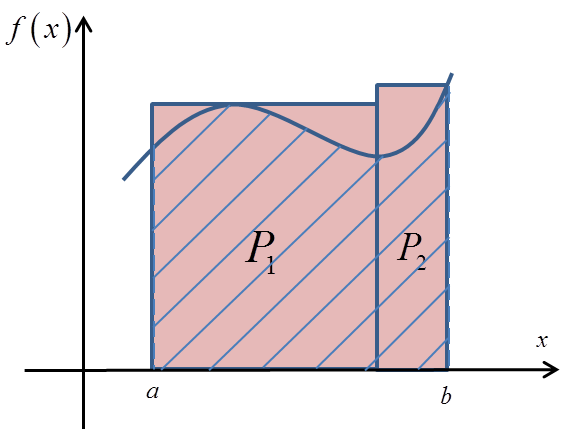
W ten sposób otrzymujemy pewne (zapewne dosyć grube) przybliżenie pola P, czyli:
![]()
Możemy pójść krok dalej i obszar przybliżyć polami trzech prostokątów:
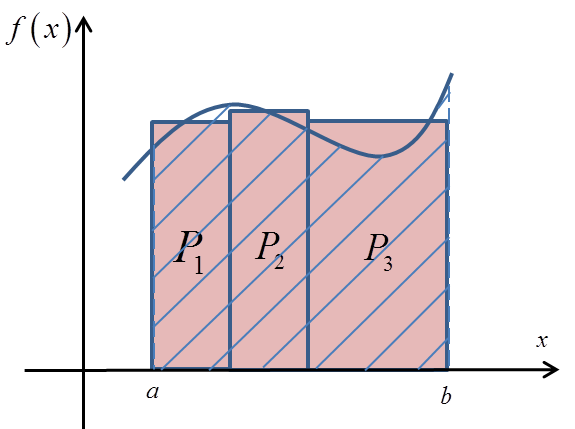
Otrzymamy oczywiście w ten sposób także przybliżenie pola P, ale zapewne już bardziej dokładne:
![]()
Zwiększając liczbę prostokątów do 10:
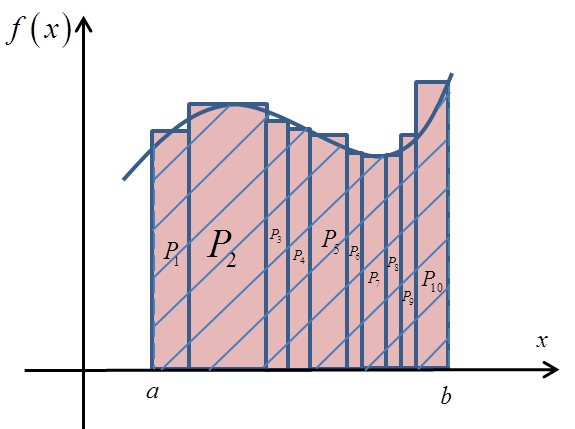
Otrzymujemy, kolejne, lepsze przybliżenie pola P:
![]()
Jeśli naszym celem było by policzenie pola P z pewną dokładnością, moglibyśmy osiągnąć to łatwo dzieląc go na odpowiednią ilość prostokątów.
Przypominam jednak, że celem jest obliczenie dokładnej, a nie przybliżonej, wartości pola P. Jak to osiągnąć?
Metoda jest już dobra, tylko prostokątów musi być po nieskończenie wiele. Jeżeli prostokątów tych będzie nieskończenie wiele i będą nieskończenie małe ich suma da nam dokładną wartość pola P.
Samo zrozumienie, że coś takiego jest możliwe, pchnęło matematykę niesamowicie do przodu.
Na tym filmiku objaśniam bliżej, jak suma nieskończonej ilości składników może być skończona, możesz przejrzeć ją sobie jako dodatek do wykładu:
Mamy w ten sposób metodę na policzenie dokładnej wartości „nietypowego” pola. Robimy to, dzieląc go na nieskończoną liczbę nieskończenie małych prostokącików i sumując ich pola.
Tak otrzymaną sumę nieskończoną (można też powiedzieć: szereg) nazywa się właśnie całką oznaczoną w sensie Riemanna (od nazwiska Pana, który jako pierwszy dobrze ją opisał).
Pozostaje już nam właściwie tylko doszlifować formalności, które powinny odpowiedzieć na kilka wiszących jeszcze w powietrzu pytań.
Zajmiemy się tym w II części Wykładu.
Część II – Definicja całki oznaczonej (jako pewnego szeregu)
Opiszmy może bardziej szczegółowo to, co robiliśmy w części I.
Na początku wybraliśmy dwa prostokąty. Aby to zrobić, musieliśmy podzielić odcinek ![]() na dwie części punktem podziału – powiedzmy –
na dwie części punktem podziału – powiedzmy – ![]() :
:
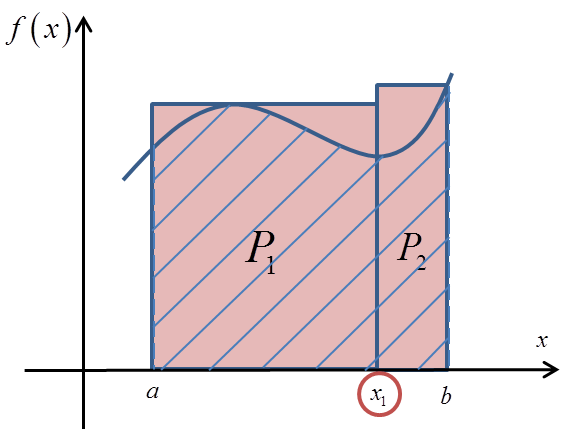
Ile równe jest pole ![]() ? Oczywiście bok razy bok. Długość jednego boku to (jak widać na wykresie)
? Oczywiście bok razy bok. Długość jednego boku to (jak widać na wykresie) ![]() . Długość drugiego boku to wartość funkcji w punkcie
. Długość drugiego boku to wartość funkcji w punkcie ![]() , czyli
, czyli ![]() :
:
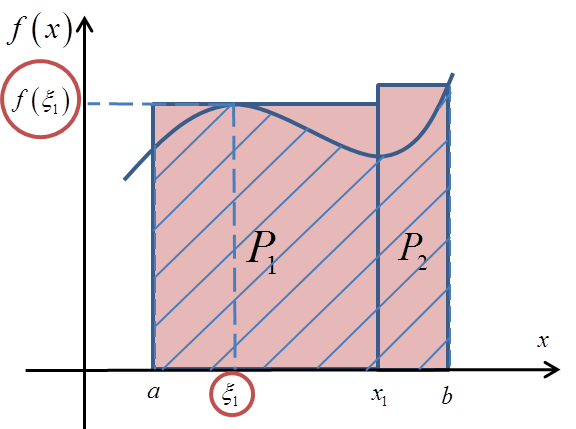
Czyli:
![]()
W przypadku pola ![]() jeden bok naszego prostokąta ma długość
jeden bok naszego prostokąta ma długość ![]() , a nasz punkt
, a nasz punkt ![]() zbiegł się właściwie z punktem
zbiegł się właściwie z punktem ![]() :
:
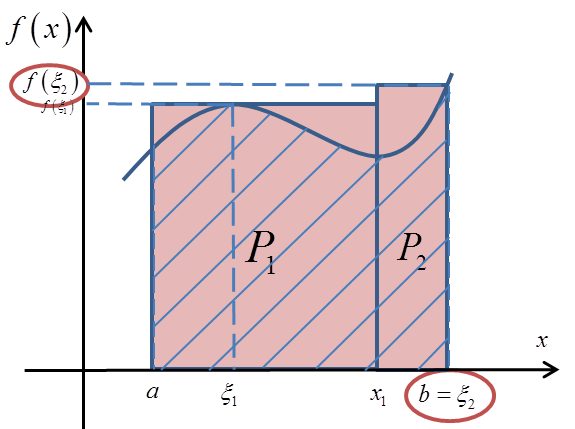
Czyli:
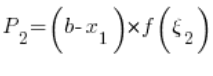
Zatem całe nasze pole P:
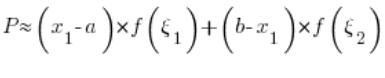
Wyczuwamy już, że konstrukcje większych ilości prostokątów będą wyglądały podobnie i zaraz się tym zajmiemy, najpierw jednak powiedzmy sobie kluczową dla całej definicji całki oznaczonej kwestię.
Uwaga.
Jeszcze raz uwaga.
Punkt ![]() dzielący odcinek
dzielący odcinek ![]() możemy wybrać sobie całkowicie DOWOLNIE. Punkt
możemy wybrać sobie całkowicie DOWOLNIE. Punkt ![]() wewnątrz odcinka
wewnątrz odcinka ![]() mogliśmy sobie wybrać całkowicie DOWOLNIE. Punkt
mogliśmy sobie wybrać całkowicie DOWOLNIE. Punkt ![]() wewnątrz odcinka
wewnątrz odcinka ![]() mogliśmy sobie wybrać całkowicie DOWOLNIE (i akurat wzięliśmy go na brzegu tego odcinka).
mogliśmy sobie wybrać całkowicie DOWOLNIE (i akurat wzięliśmy go na brzegu tego odcinka).
Oznacza to, że gdybyśmy przyjęli zupełnie inne punkty ![]() ,
, ![]() , otrzymalibyśmy zupełnie inne prostokąty:
, otrzymalibyśmy zupełnie inne prostokąty:
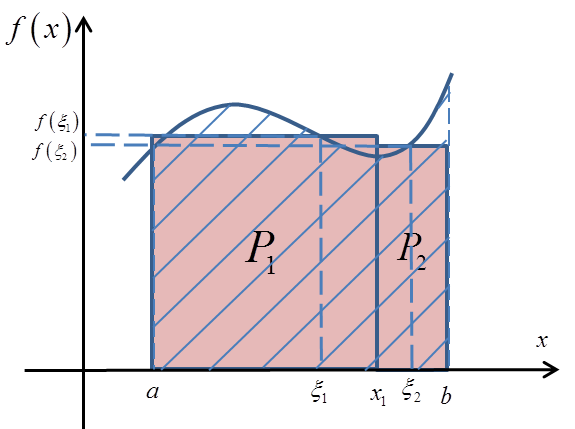
Jednak pola tych prostokątów nadal w pewien sposób stanowiły by przybliżenie pola P (oczywiście inne, niż poprzednim razem) i stosując naszą metodę dalej (zwiększając liczbę prostokątów w nieskończoność) otrzymalibyśmy równie dobrze pole obszaru P.
Przybliżmy teraz pole P trzema prostokątami, tak jak robiliśmy to w części I.
Zwiększając liczbę prostokątów do trzech dzielimy odcinek ![]() na trzy dowolnie wybranymi punktami
na trzy dowolnie wybranymi punktami ![]() ,
, ![]() i wewnątrz nich dowolnie wybieramy punkty
i wewnątrz nich dowolnie wybieramy punkty ![]() :
:
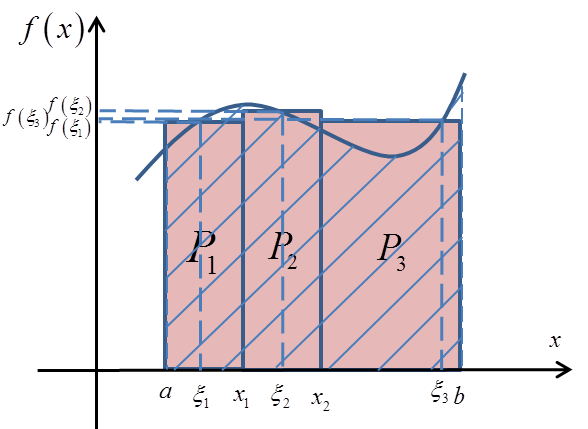
Otrzymując w ten sposób przybliżenie pola P:
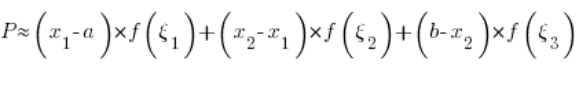
Odcinki: 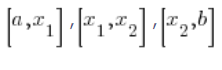 możemy dla skrócenia oznaczyć jako:
możemy dla skrócenia oznaczyć jako:
![]() .
.
Mamy więc:
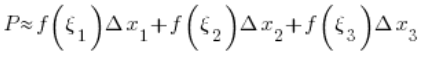
Widzimy więc, że dla jakiegokolwiek ustalonego podziału na 'n’ prostokątów mamy:
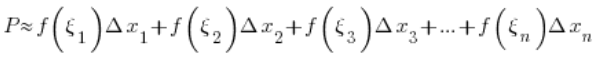
DEFINICJA CAŁKI OZNACZONEJ
Zwiększając liczbę odcinków, na które dzielimy odcinek ![]() w nieskończoność otrzymujemy sumę nieskończoną (zwaną: „sumą całkową”):
w nieskończoność otrzymujemy sumę nieskończoną (zwaną: „sumą całkową”):
Jeśli ta granica zbieżna jest zawsze do tej samej liczby, niezależnie od wyboru odcinków ![]() (przy czym zakładamy, że długości tych odcinków dążą do zera wraz ze wzrostem
(przy czym zakładamy, że długości tych odcinków dążą do zera wraz ze wzrostem ![]() ) i niezależnie od wyboru punktów
) i niezależnie od wyboru punktów ![]() , to liczba ta nazywa się całką oznaczoną w przedziale od a do b.
, to liczba ta nazywa się całką oznaczoną w przedziale od a do b.
Zwróć uwagę na nieprzypadkowe podobieństwo oznaczeń:
oraz:
![]()
Całkowanie to nic innego jak sumowanie. Sumowanie wartości nieskończenie małych.
Zwróćmy jeszcze raz uwagę na istotne punkty definicji:
- Długość odcinków
 musi być nieskończenie mała, tzn. jeśli przez
musi być nieskończenie mała, tzn. jeśli przez  oznaczymy długość najdłuższego z nich dla danego n, to musi być:
oznaczymy długość najdłuższego z nich dla danego n, to musi być:  . Inaczej moglibyśmy obrać sobie na początku jakiś prostokąt na przykład
. Inaczej moglibyśmy obrać sobie na początku jakiś prostokąt na przykład  i całą resztę obszaru podzielić na nieskończenie małe prostokąty. Mielibyśmy wtedy nieskończoną ilość prostokątów, ale nie mielibyśmy dokładnej wartości pola P.
i całą resztę obszaru podzielić na nieskończenie małe prostokąty. Mielibyśmy wtedy nieskończoną ilość prostokątów, ale nie mielibyśmy dokładnej wartości pola P. - Podział odcinka
 na nieskończenie małe odcinki
na nieskończenie małe odcinki  musi być całkowicie dowolny, tak samo jak wybór punktów
musi być całkowicie dowolny, tak samo jak wybór punktów  i dla każdego takiego wyboru szereg musi sumować się do tej samej liczby. Jeżeli dla jednego wyboru odcinków i punktów wychodzi nam inna wartość sumy, niż dla wszystkich pozostałych ta suma nie jest całką oznaczoną.
i dla każdego takiego wyboru szereg musi sumować się do tej samej liczby. Jeżeli dla jednego wyboru odcinków i punktów wychodzi nam inna wartość sumy, niż dla wszystkich pozostałych ta suma nie jest całką oznaczoną.
Aby nabrać wprawy i zrozumienia definicji całki oznaczonej, na kolejnym wykładzie przejdziemy do przykładów na obliczanie całek oznaczonych z definicji.
KONIEC
Pisząc tego posta korzystałem z…
1. „Rachunek różniczkowy i całkowy. Tom II.” G.M. Fichtenholz. Wyd. 1966.
Kliknij, aby powrócić na stronę z wykładami o całkach oznaczonych

madzia
Witam mam pytanie odnośnie granic całokowania jesli za pomoca całki chcemy opliczyc pole koła. pierwsza calka ma granice od r do zera a druga od 2\pi do 0?(układ sferyczny) A cała całka wynosi[rsin(x)]?
Michał
Mialbym jeszcze jedno pytanie 🙂 czemu nie mozemy wykorzystywac tej metody z suma nieskonczonej ilosci prostokatów w przypadku całki nieoznaczonej ????
Bo ten sposob pokazal pan w przypadku całki oznaczonej ale czemu nie moze byc on wykorzystywany przy całce nieoznaczonej ????
Krystian Karczyński
Ta metoda z nieskończoną ilością prostokątów jest w praktyce BARDZO męcząca i trudna (zerknij na mój następny Wykład). Dlatego o wiele, wiele prościej jest skorzystać z tw. Newtona-Leibnitza (czyli w praktyce z całki nieoznaczonej).
Michał
Teraz rozumiem czyli to od nasz zalezy wybor metody 🙂 jezeli mamy całke nieoznaczona mozemy korzystac z metody z wczesniejaszego wykładu a jezeli oznaczona to z tego powyzej 🙂 dziekuje bardzo bo bardzo mnie to zastanawialo 🙂 Dziekuje za odpowiedz i za wytłumaczenie 🙂
Michał
Mam jedno pytanie na wcześniejszym wykładzie o całkach nieoznaczonych a dokładnie
,, całki nieoznaczone a pola figur ” tłumaczył pan w inny sposób jak liczyc pola nietypowych obszarów za pomoca stwierdzenia ze pierwsza funkcja jest pochodną drugiej. Czy ma ona jakis związek z tym drugim sposobem liczenia za pomoca sumy nieskonczenie wielu prostokątów ???? Ja słyszalem na wykładach tylko o tej jednej metodzie dlatego \interesuje mnie skad jest ten 2 sposob ??? Czy to zalezy od całki ktora metode wykorzystujemy ????
i czy sa one jakos powiazane ????
Krystian Karczyński
Jasne, że jest, do problemu obliczenia pola można podejść na dwa sposoby.
Całkę nieoznaczoną i całkę oznaczoną łączy wzór Newtona – Leibnitza:
[pmath]int{a}{b}{f(x)dx}=F(b)-F(a)[/pmath]
Po lewej stronie równości jest całka oznaczona (czyli pole liczone w wykładzie powyżej), a po prawej funkcje pierwotne (czyli całki nieoznaczone, liczone w wykładzie o całkach nieoznaczonych i polach).
Klaudia
Dziękuję bardzo 🙂
Klaudia
Witam
Chciałabym się zapytam, jak dobrze przesuwać granice całkowania? W Pana kursie, najpierw obliczamy całkę nieoznaczoną, potem podstawiamy do uzyskanego wyniku granice całki. Na mojej uczelni, nie dzielą całki oznaczonej na nieoznaczoną, i jak mają oznaczoną to obliczają ją zwyczajnie z granicami, tylko one są w jakiś sposób przesuwane. Nigdy do końca nie jestem pewna czy zrobiłam dobre przesunięcie, więc liczę Pana sposobem, ale dowiedziałam się, że na egzaminie mogę mi tego nie uznać ;p
PS Reguły Sarrusa też mam ponoć lepiej nie stosować, bo mogę punktów nie dostać;p
Krystian Karczyński
Dzień dobry
Tutaj jest post na ten temat:
Zmiana granic całkowania
Różne takie mity, że „mogą nie uznać” czegoś tam oczywistego zawsze chodzą po ludziach… Najlepiej je sprawdzać u źródła, tzn. pytając wprost egzaminatora (oczywiście odpowiednio wcześnie, a nie podczas rozdawania kartek z pytaniami) 🙂