Post jest jakąś formą odpowiedzi na pytanie w komentarzach do powyższego filmiku na Youtubie ( link do komentarza ):
czegoś nie rozumiem i proszę o wytłumaczenie, czemu skracasz „n” ? chodzi mi o to że n/n jest to symbol nieoznaczony (nieskończoność przez nieskończoność) help bo już się tym pogubiłem
Zrozumienie, czym NAPRAWDĘ są symbole nieoznaczone sprawia wiele kłopotów. Rodzi się także wiele pytań o to, co „wolno” z nimi robić, a czego „nie wolno”.
Mała powtórka
Przypomnijmy je najpierw:
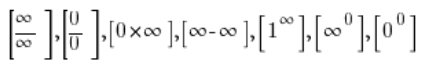
Jak już na pewno wiele razy słyszeliście w symbolach nieoznaczonych:
– znaczek ![]() nie oznacza tutaj jakiejś „liczby”, ani w ogóle jakiegoś obiektu matematycznego, tylko SYMBOLIZUJE rozbieganie do nieskończoności (nieskończoność nie jest liczbą!)
nie oznacza tutaj jakiejś „liczby”, ani w ogóle jakiegoś obiektu matematycznego, tylko SYMBOLIZUJE rozbieganie do nieskończoności (nieskończoność nie jest liczbą!)
– znaczek ![]() nie oznacza wcale liczby
nie oznacza wcale liczby ![]() , tylko SYMBOLIZUJE zbieganie do zera
, tylko SYMBOLIZUJE zbieganie do zera
– znaczek ![]() nie oznacza wcale liczby
nie oznacza wcale liczby ![]() , tylko SYMBOLIZUJE zbieganie do 1
, tylko SYMBOLIZUJE zbieganie do 1
– symbol nieoznaczony ![]() nie oznacza wcale dzielenia jakiejś „liczby” przez jakąś „liczbę”, tylko SYMBOLIZUJE sytuację, w której licznik i mianownik rozbiegają do nieskończoności
nie oznacza wcale dzielenia jakiejś „liczby” przez jakąś „liczbę”, tylko SYMBOLIZUJE sytuację, w której licznik i mianownik rozbiegają do nieskończoności
– itd.
Mając więc do policzenia granicę:
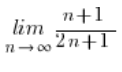
…możemy powiedzieć, że mamy w niej symbol nieoznaczony ![]() , ponieważ licznik i mianownik w wyrażeniu rozbiegają do
, ponieważ licznik i mianownik w wyrażeniu rozbiegają do ![]() .
.
W wyrażeniu ![]() NIE możemy sobie nieskończoności „skrócić”, ponieważ w wyrażeniu nieoznaczonym NIE oznaczają one w ogóle liczb, które można by „skracać’ ,wykonywać na nich działania itp.
NIE możemy sobie nieskończoności „skrócić”, ponieważ w wyrażeniu nieoznaczonym NIE oznaczają one w ogóle liczb, które można by „skracać’ ,wykonywać na nich działania itp.
W wyrażeniu 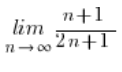 również nie możemy na starcie czegoś „skrócić”, ale nie dlatego, że są jakieś przyczyny formalne – ale po prostu dlatego, że nic się nie skraca 🙂
również nie możemy na starcie czegoś „skrócić”, ale nie dlatego, że są jakieś przyczyny formalne – ale po prostu dlatego, że nic się nie skraca 🙂
Trzeba więc stosować jakieś metody (w tym przypadku akurat wyciągać przed nawias – co opisałem w moim Kursie Granic), kombinować itd.
Weźmy jednak trywialną granicę:
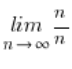
Jest to właściwie również granica, w której mamy symbol nieoznaczony ![]() – bo licznik i mianownik dążą do nieskończoności.
– bo licznik i mianownik dążą do nieskończoności.
W wyrażeniu ![]() również NIE możemy sobie nieskończoności „skrócić”, ale tym razem…
również NIE możemy sobie nieskończoności „skrócić”, ale tym razem…
Skróty możemy wykonać i to jak najbardziej w wyrażeniu 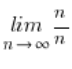 .
.
'n’ jest to jak najbardziej zmienna matematyczna, na której można wykonywać operacje arytmetyczne, skracać itd. (w odróżnieniu od symbolu ![]() ). Czyli
). Czyli ![]() i wszystko jest czysto i legalnie.
i wszystko jest czysto i legalnie.
Podsumowując
Na obiektach ![]() W SYMBOLACH NIEOZNACZONYCH nie można wykonywać operacji arytmetycznych, skracać ich itp.
W SYMBOLACH NIEOZNACZONYCH nie można wykonywać operacji arytmetycznych, skracać ich itp.
Na obiektach ![]() W WYRAŻENIACH, z których liczymy granicę ciągów i funkcji zdecydowanie można wykonywać operacje matematyczne, skracać je itd.
W WYRAŻENIACH, z których liczymy granicę ciągów i funkcji zdecydowanie można wykonywać operacje matematyczne, skracać je itd.
Mam nadzieję, że nie zamotałem Cię jeszcze bardziej, ClumsyFriday, powodzenia z granicami!


7 Komentarzy
torpeda121
Witam Panie Krystianie, super tłumaczy Pan pojęcia matematyczne, ale pojawił się mi dylemat, czy ile wynosi granica wyrażenia: A/0, przy założeniu, że A jest dodatnie, a ile gdy ujemne?
Pozdrawiam i proszę o odpowiedź
Krystian Karczyński
To zależy od tego, czy w mianowniku jest liczba dodatnia, czy ujemna.
Bo z tym, że w mianowniku nie ma dokładnie równo liczby 0 to się zgadzamy? 🙂
https://blog.etrapez.pl/granice/granica-ciagu/dzielenie-przez-zero/
Łukasz
Ja mam pytanie odnośnie monotoniczności funkcji. Zabrakło mi tam działań z pierwiastkami i np. nie wiem jak wyciągnąć mam „iks” z pierwiastka 2 stopnia z x(2) + x + 1 ;/
Krystian Karczyński
Sorry, ale nie do końca zakumałem.
Chodzi o wyciąganie „x” przed nawias w jakiejś granicy? Czy o rozwiązanie równania:
[pmath]sqrt{x^2+x+1}=0[/pmath] ?
Mógłbyś zapodać całe zadanie z poleceniem?
ClumsyFriday
Jestem naprawdę mile zaskoczony, że odpowiadasz na tak banalne pytania(teraz takie mi się już wydają). Zakupiłem kurs wszystko jest jasne jak słońce. To co robisz wychodzi Ci świetnie. Serdecznie dziękuje. 🙂 Polecam wszystkim kursy, naprawdę warto, idealnie uzupełniają to czego nie zrozumiałeś do końca na wykładzie.
Krystian Karczyński
Na banalne pytania w matematyce najtrudniej się odpowiada, serio 🙂
Dzięki za zakup Kursu i za polecenia, cieszę się, że się przydaje.
Krystian Karczyński
Panie Kazimierzu, przepraszam, że nie odpowiedziałem na maile.
Niestety, w ogóle się nie orientuję w tematyce Pańskich opracowań, nie potrafię Panu w żadne sposób pomóc., bardzo mi przykro.