Asymptoty Wykład 4
Temat: “Sławne” asymptoty funkcji
Streszczenie
Temat asymptot na studiach nie jest czymś zupełnie nowym. Wiele znanych od czasów szkoły średniej wykresów funkcji posiada asymptoty, które wyznaczać można nawet bez obliczania granic. Na wykładzie powtórzymy sobie kilka popularnych funkcji z asymptotami.
Asymptoty funkcji trygonometrycznych
Przyjrzyjmy się wykresowi funkcji ![]() :
:
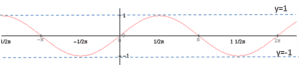
Źródło obrazka: Wikipedia (licencja public domain)
Jak myślisz, czy proste y=1 i y=-1 są równaniami asymptot wykresu?
Prawidłowa odpowiedź to: oczywiście NIE. Dlaczego?
Pozostając na gruncie intuicyjnego rozumienia asymptoty: miało być to “coś” do czego przybliża się coraz bardziej wykres funkcji. Na wykresie sinusa widać zaś, że wykres funkcji zamiast przybliżać się do prostej y=1/y=-1 rytmicznie się od niej oddala i znów przybliża.
A teraz będąc bardziej ścisłym, prosta y=a była równaniem asymptoty poziomej funkcji f(x), wtedy, gdy istniała granica:
![]()
W naszym zaś przypadku granica funkcji sinusx przy ![]() :
:
![]() – nie istnieje.
– nie istnieje.
Jasnym jest, że to samo tyczy się cosinusa x.
Asymptoty pionowe posiadają zaś funkcja tgx:
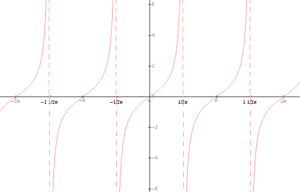
Źródło obrazka: Wikipedia (licencja public domain)
Widać, że funkcja ta ma nawet nieskończenie wiele asymptot pionowych obustronnych o równaniach: ![]() , gdzie k jest dowolną liczbą całkowitą. Przykładowe równania tych asymptot to więc:
, gdzie k jest dowolną liczbą całkowitą. Przykładowe równania tych asymptot to więc: 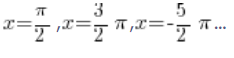
Jeżeli chcemy więc obliczyć równania asymptot pionowych funkcji tangens x, trzeba przyrównać jego argument do ![]() i rozwiązać równanie (wiąże się to oczywiście z wyznaczeniem dziedziny tangensa).
i rozwiązać równanie (wiąże się to oczywiście z wyznaczeniem dziedziny tangensa).
Przykład
Wyznacz równania asymptot funkcji 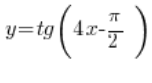
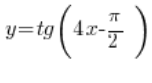
Przyrównujemy argument tangensa do ![]()
![]()
![]()
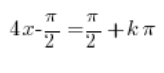
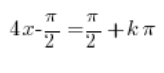
Przenosimy ![]()
![]()
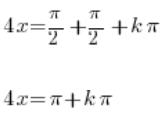
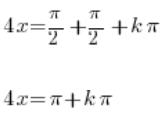
Dzielimy obustronnie przez 4:
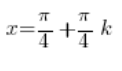
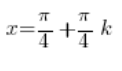
A powyższe to właśnie równania asymptot pionowych obustronnych, które mieliśmy wyznaczyć.
Asymptoty pionowe ma także funkcja ctgx:
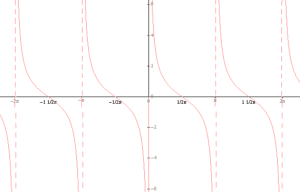

Źródło: Wikipedia (licencja public domain)
Ich równaniami będą proste: ![]()
![]()
Asymptoty funkcji cyklometrycznych
Funkcje cyklometryczne to funkcje odwrotne do trygonometrycznych. Oznaczamy je: arcsinx, arccosx, arctgx, arcctgx. Skoro funkcje sinx i cosx nie posiadały asymptot, to raczej trudno, żeby odwrotne do nich je miały 🙂
Asymptoty poziome będzie miał natomiast wykres funkcji arctgx:
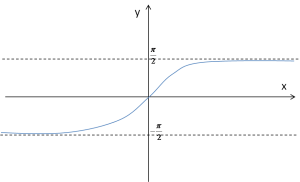

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Asymptoty poziome będzie miał także wykres funkcji arcctgx:
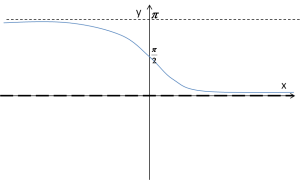

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Asymptoty funkcji wykładniczych
Przez “funkcję wykładniczą” rozumieć będziemy funkcję ![]()
![]()
Jeżeli a>1 jej wykres będzie wyglądał w przybliżeniu tak:
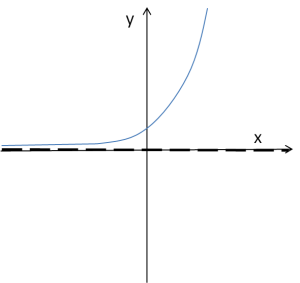

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Jeżeli zaś a<1 wykres przyjmie postać:
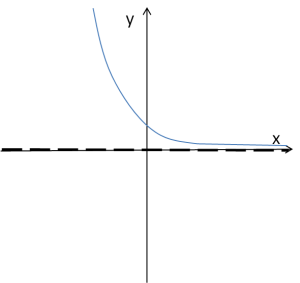

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Asymptoty funkcji logarytmicznych
Funkcje logarytmiczne, o równaniach ![]()
![]()
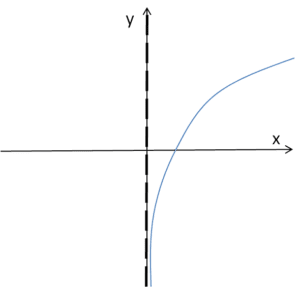

Wykres funkcji logarytmicznej dla a>1
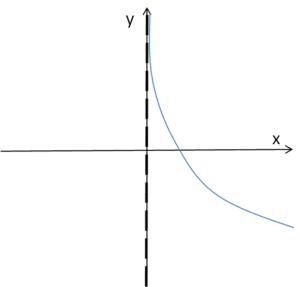

Wykres funkcji logarytmicznej dla a<1
Widać, że niezależnie od a prosta ![]()
![]()
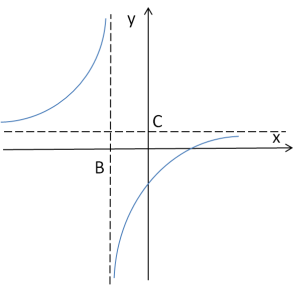
Asymptoty funkcji homograficznych
Z funkcjami homograficznymi spotkaliśmy się w szkole średniej. Były to szczególne rodzaje funkcji wymiernych, postaci:
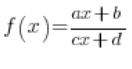
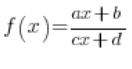
Przy pomocy specjalnych przekształceń doprowadzało się tą funkcję do tzw. “postaci kanonicznej”:
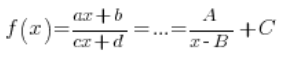
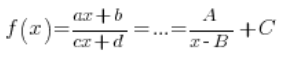
Z której to od razu można odczytać było równanie asymptoty poziomej: ![]()
![]()
![]()
![]()
A na wykresie wyglądało by to tak:

Kliknij, aby przejść do określenia, czym są ekstrema funkcji (następny Wykład) –>
Kliknij, aby powrócić na stronę z wykładami o badaniu przebiegu zmienności funkcji


Jakie asymptoty będzie maiła funkcjag(x)=1/tanx
Ile maksymalnie asymptot ukośnych bądź poziomych może mieć funkcja?
ok już wiem 2
Panie Krystianie a czy wykres z log przy podstawi a = pi/3 bedzie rosnący czy malejący ?
Rosnący, bo \pi /3jest większe od 1.
Ale prawidłowo powinno się powiedzieć, że to FUNKCJA będzie rosnąca (a nie “wykres”).
Witaj!
Mam pytanie a właściwie problem z obliczeniem asymptot funkcji. Mam taką funkcję: http://latex.codecogs.com/gif.latex?%5Cfrac%7Bx%5C\sqrt%7Bx%7D%7D%7B%5C\sqrt%7Bx%7D-1%7D
Oczywiście dziedzina to <0;1) u (1;inf).
I tu moje pytanie, skoro asymptoty liczymy na skraju funkcji, to czy w tym przypadku powinno się ją liczyć w punkcie 0, czy nie?
Witam, oczywiście nie, asymptoty liczymy “na skraju”, czyli trzeba liczyć w punkcie 1.